若将物体分割成许多微小部分,则在重力场中,其每一部分都要受到重力ΔPi 的作用。在图3-23所示坐标下,设其作用点为Mi (xi,yi,zi)(i=1,2,…,n)。
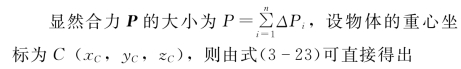
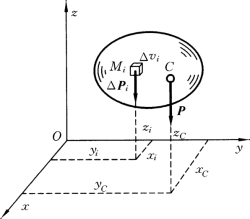
图3-23

可见,物体分割得越细,即每小块体积越小,则按式 (3-24)计算出的重心位置就越精确,在极限情况下可用积分计算,即

对于均质物体,设其密度为ρ,若分割成有限部分,第i块体积为ΔVi,整体体积为V,则由式(3-25)可得
式 (3-26)表明,均质物体的重心位置完全取决于物体的几何形状。而与物体的重量无关,这时C点也往往称为形心。
在极限情况下,均质物体的重心坐标可由式(3-25)直接得出,即

对于均质等厚薄板,类似地可得重心公式

对于均质线段,类似地可得重心公式

【例3-7】 求图3-24所示三角形的重心。
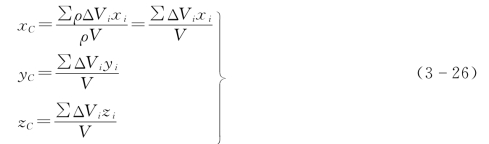
解:取图3-24所示坐标系Oxy,可用积分法求出重心的坐标 (xC,yC)。若先确定重心C的y坐标yC,则可取微元dS=a1dy,a1 为微元dS的宽度。根据公式(3-28)得

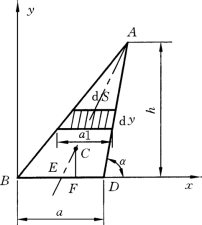
图3-24(https://www.xing528.com)
由本例可以看出,规则形体的重心位置总可以较容易地用积分法确定,故简单物体的形心位置均可通过积分法求得。
前面是通过积分公式确定物体的重心坐标,如果物体很不规则,积分将会遇到困难。但有些物体由于有其特殊性,如对称性或可划分成几个规则形体等,则这时可经过特殊分析处理,使其重心位置的确定更加简单。
如对于对称物体,由于其具有对称轴、对称面或对称中心等,则其重心必在物体的对称轴、对称面或对称中心上,其具体位置进一步可由前述公式确定。
对于组合形体,尽管它们不很规则,但一般说它们是由若干个简单形体组合而成的,若已知简单形体的重心,则整个组合形体的重心就可用式 (3-26)直接求出。这时的体积、面积和长度可以有正负值。这比用积分法要简单得多。
【例3-8】 试求Z字形截面重心的位置,尺寸如图3-25所示。
解:取坐标轴如图所示,将Z字形截面分为三个部分,每部分都是矩形,若矩形的面积用Ai表示 (i=1,2,3),其质心坐标用(xi,yi)表示,则
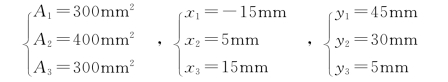
将这些数据代入式(3-26),得到Z字形截面重心位置为
![]()
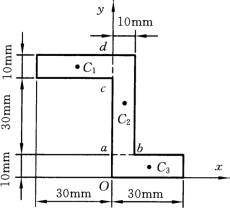
图3-25
![]()
【例3-9】 已知振动器中的偏心块的几何尺寸,r1=10cm,r2=3cm,r3=1.7cm,求偏心块重心的位置(见图3-26)。
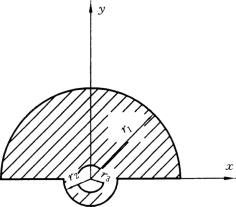
图3-26
解:本题仍是平面图形的重心问题,由于此图形具有对称轴,取坐标系如图3-26所示,则显然有xC=0。yC 可用组合法求出:将整个图形看成由三部分组成,即半径为r1 的半圆,半径为r2 的半圆以及半径为r3 的小圆,圆与半圆均属简单图形,利用式 (3 26)就可求出重心位置坐标。但是按这种分割方法,小圆实际上并不在图形上,如果用两半圆的面积代入公式中所确定的质心坐标将整整多出了小圆面积的影响,故计算中应把小圆去掉,即应减去小圆面积对重心的影响,这时,只要把小圆的面积用负值代入,便会得到本图形的重心坐标。
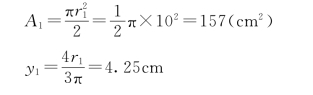
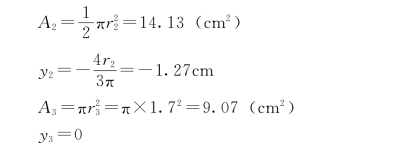
于是,整个物体重心坐标为
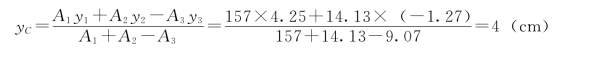
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




