求解空间力系的平衡问题,其步骤与求解平面力系一样,一般仍是先确定研究对象,进行受力分析并作出受力图,选取适当的坐标系,列出平衡方程并求解未知量。在一般情况下,空间力系有六个独立的平衡方程,它可求解六个未知量,在求解中,投影和取矩轴可视解决问题的方便适当选取,这样就可以使每一平衡方程中包含的未知数最少,计算得以简化。另外,有时为了方便,也可减少平衡方程中的投影方程,而将平衡方程表示为四力矩形式以至六力矩形式。但这时投影轴与力矩轴之间要有一定的限制,这里不再详述。
【例3-4】 如图3-19 (a)所示为一简易起吊装置,杆AB的A端为球形铰链支座,另一端B装有滑轮,并用系在墙上的绳子CB 和DB 拉住,若已知γ=30°,β=45°,P=10kN,DBC在水平面上且DE=CE=BE=a,求杆AB和绳子CB、BD的内力。
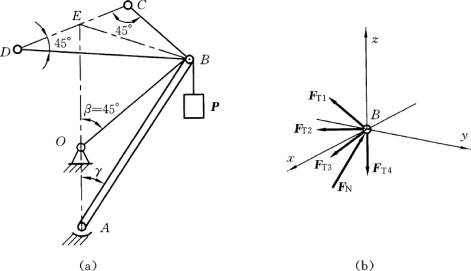
图3-19
解:(1)以滑轮B为研究对象。
(2)受力分析:因杆AB不计自重,且只在两端受力,故AB为二力杆;作用在B上的力有:杆AB对滑轮的力FN,各绳子的拉力FT1,FT2,FT3和FT4,如图3-19 (b)所示,由于不计滑轮尺寸,则可将B处的力视为汇交力系。若取B点为坐标原点,建立图示坐标系。则平衡方程为
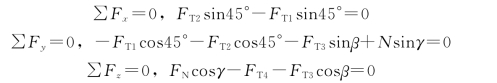
将FT3=FT4=10kN,γ=30°,β=45°代入,解上面三个方程得
![]()
杆AB的内力与FN 大小相等,方向相反,且为压力,绳子CB和BD 的内力也分别与FT1和FT2互为作用与反作用力。
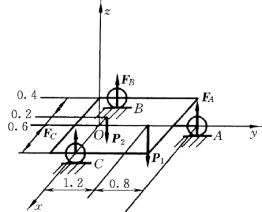
【例3-5】 如图3-20所示三轮车自重P1=8kN,载荷P2=10kN,且P2 作用在B,C两轮连线上,求地面对三个轮子的约束反力。图中长度单位为m。
解:(1)取三轮车为研究对象。
(2)受力分析:三轮车在静止时,只受重力P1,载荷P2 和地面的约束反力FA,FB 和FC 作用。这些力构成一空间平行力系,若取坐标系Oxyz如图3-20所示,则利用空间平行力系平衡方程得
 (https://www.xing528.com)
(https://www.xing528.com)
图3-20
![]()
![]()
代入已知数据并联立求解得

【例3-6】 悬臂刚架如图3-21所示,其上作用着q=2kN/m的均布荷载,以及作用线分别平行于AB、CD的集中力P、Q。已知P=5kN,Q=4kN,求固定端O处的约束反力。
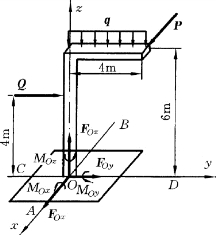
图3-21
解:(1)取悬臂刚架为研究对象。
(2)受力分析:刚架除受到P、Q和均布荷载q外,在O处还受约束反力作用,由于O处为固定端约束,此处反力的分布应为空间一般力系,若向O点简化便得一主矢量FO和一主矩MO。现过O点作一坐标系,如图3-21所示,则可将FO、MO 均用其在坐标轴方向的分量表示,即FOx、FOy、FOz和MOx、MOy、MOz,这六个量就是O处的反力。
根据空间一般力系的平衡方程得
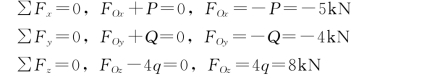
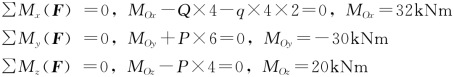
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




