空间力系简化原理-理论力学

空间力系向空间内任一点简化的过程与平面力系的简化过程类似，力的平移定理仍然适用，只是在平移时，由于力线位置的任意性，力线与平移点所构成的平面的方位就各不相同，所以平移后，附加力偶必须用矢量表示，且其力偶矩矢就等于力对平移点的力矩矢，即M =MO （F）。设在刚体上各点A1、A2、…、An 作用有空间任意力系F1、F2、…、Fn，如图3-12所示，任取一点O作为简化中心，将各力向O点平移，这样就会得到一个作用在O点的空间汇交力系F′1、F′2、…、F′n 和由各附加力偶组成的附加力偶系，如图3-12所示，显然，由力的平移定理知：F′1=F1、F′2=F2、…、F′n=Fn 各附加力偶矩矢就等于原力系中各力对简化中心O 点的矩矢，且分别为MO（F1），MO（F2），…，MO（Fn）。

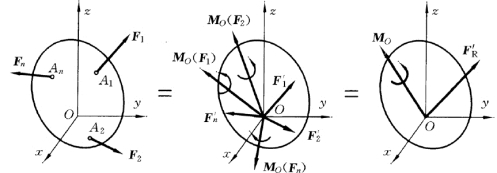
图3-12

上述空间汇交力系和空间力偶系可进一步合成，空间汇交力系可合成一个作用于简化中心（O点）的力F′R，且等于原力中各力的矢量和，即

式中：F′R 为原力系的主矢量。

附加力偶系可合成为一个空间力偶，其力偶矩矢MO 等于各附加力偶矩矢的矢量和，也等于各力对简化中心的矩的矢量和，即

式中：MO 为原力系对简化中心O 的主矩。

力系的主矢量与简化中心的选择无关，而力系对简化中心的主矩则随简化中心选取的不同而改变。

综上所述可得结论：空间一般力系向空间内任一点简化，可得到一个力和一个力偶，此力作用在简化中心，称为原力系的主矢量，它等于原力系中各力的矢量和；这个力偶的力偶矩矢称为原力系对简化中心的主矩，它等于原力系中各力对简化中心的矩的矢量和。(www.xing528.com)

为了计算方便，一般在求主矢量、主矩时利用解析法进行，这时如以简化中心为坐标原点，取直角坐标系Oxyz，如图3-12所示，将式 （3-15）的两边分别在三个坐标轴上投影，可得

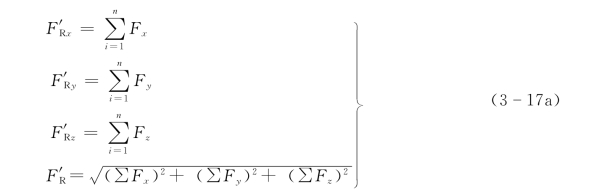
若主矢的方向角用α、β、γ表示，则主矢的方向余弦为

同样将式（3-16）的两边向三个坐标轴上投影，并利用力对点的矩与力对轴的矩间的关系，可得

若以λ、μ、ν表示主矩的方向角，则主矩的方向余弦为

此时，可以证明合力矩定理仍然成立，空间一般力系的合力对任意一点（轴）的矩等于力系中各分力对该点（轴）的矩的矢量和（代数和）。