【摘要】:对于平面问题,由于力的作用线和矩心所组成平面总是在一个方位上,故力对点的矩可用代数量表示,也就是说力对点的矩只与力矩的大小和转向有关。但是,对于空间力系,各力作用线与同一矩心所组成的平面的方位一般是不同的,这时力使物体绕矩心的转动效应就不仅取决于力矩的大小和转向,还取决于力矩平面的方位。这三个要素决定了力对点的矩必须用矢量表示。即力对任一点的矩等于该力作用点对于矩心的矢径与该力的矢量积。
对于平面问题,由于力的作用线和矩心所组成平面总是在一个方位上,故力对点的矩可用代数量表示,也就是说力对点的矩只与力矩的大小和转向有关。但是,对于空间力系,各力作用线与同一矩心所组成的平面的方位一般是不同的,这时力使物体绕矩心的转动效应(力对点的矩)就不仅取决于力矩的大小和转向,还取决于力矩平面的方位。因为,若方位不同,即使力矩的大小相同,它们对物体的作用效应也将完全不同。在空间力系中,力对点的矩的概念应包括三个要素,即力矩的大小、力矩在其平面内的转向以及力矩平面的方位。这三个要素决定了力对点的矩必须用矢量表示。其表示方法如下:

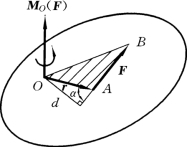
图3-10
![]()
根据上述定义,力矩矢与矩心位置有关,当矩心的位置不同时,力矩矢的大小和方向都将随之改变,图3-10中MO(F)只能画在O点,因而力矩矢为一定位矢量。

即力对任一点的矩等于该力作用点对于矩心的矢径与该力的矢量积。(https://www.xing528.com)
利用矢积式 (3-10)可以得出力矩MO(F)解析表达式。为此,以矩心O为原点建立空间直角坐标系Oxyz,如图3-11所示。
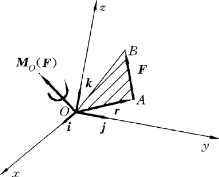
图3-11
设坐标轴的单位矢量是i、j、k,A点的坐标为A(x,y,z),F在坐标轴上的投影为Fx,Fy,Fz,则r与F的解析式为
![]()
于是
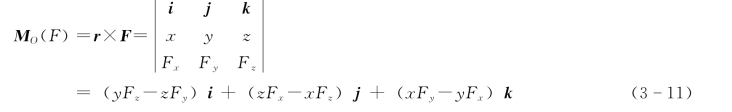
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




