力对轴的矩及其计算方法

在生产和生活实际中，常遇到有些物体在力的作用下绕某轴转动，应该怎样表示力对转动体的效应呢？这就提出一个新的概念，即力对轴的矩。

现以开门为例来说明力对轴的矩的概念。如图3-7所示，门受A点一任意方向力F 作用而绕门轴转动。为了确定其转动效应，可将力F分解为平行于门轴和垂直于门轴方向的分力F′与F″，实践证明无论力F′的大小如何，均不能使门绕门轴转动，而使门转动的只是分力F″，所以力F对门的转动效应等于其分力F″对门的转动效应。若过力F″的作用线作一与门轴垂直的平面，该平面与门轴交于O点，则这时可用分力F″对O 点的矩MO（F″）来表示力F对门的转动效应。

由此可见，在一般情况下，力使物体绕某轴转动的效应可用此力在垂直于该轴的平面上的分力对此平面与该轴的交点的矩来度量。我们就把这个力矩称为力对轴的矩，并用Mz （F）表示，即

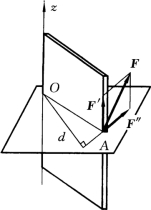
图3-7

式中：d为O 点到F″作用线的垂直距离。

力对轴的矩是一个代数量，其正负号表示力使物体绕转轴转动的转向，且符合右手螺旋规则，即四指与转向一致时握拳，拇指的指向如与z轴的正向相同，则该力对轴的矩为正，反之为负。力对轴的矩的单位为牛顿·米 （Nm）。

从式（3-8）可知：

（1）当力的作用线与轴平行（F″=0）或相交 （d=0），亦即力与轴位于同一平面时，力对该轴的矩等于零。

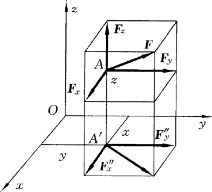
图3-8

（2）当力沿其作用线移动时，它对轴的矩不变，这是因为此时F″和d均未改变。

在计算力F对z轴的矩时，若求F″和d不太方便，则式（3-8）不便于应用。这时可以应用合力矩定理，将F″分解为F″x 和F″y （如图3-8所示）两个分力，再求出它们对O点的矩的代数和，即(www.xing528.com)

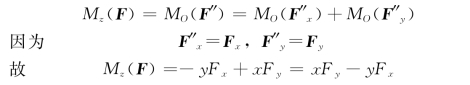
依照同样方法，也可以得到F对x轴和y轴的矩的表达式。力F对x，y，z轴的矩分别为

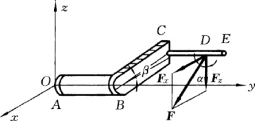
图3-9

从图3-8可以看出，式 （3-9）中的Fx，Fy，Fz，x，y，z都是正值，若它们中有的为负值时，则以负值代入，公式依然成立，这说明式（3-9）中各量都是代数值。

【例3-3】 手柄ABCE所在平面与水平面的交角为β，在D处作用一力F，如图3-9所示，它在垂直于y轴的平面内，偏离铅直线的角度为α。如果CD=a，杆CE平行于y轴，BC垂直AB，且AB=BC=l，试求力F对x，y，z三轴的矩。

解：先将力F分解到坐标轴上，求出分力，计算分力对各轴的矩，再利用合力矩定理给出所求。由于F位于垂直y轴的平面内，故F在坐标轴上的分力将只有Fx 和Fz。

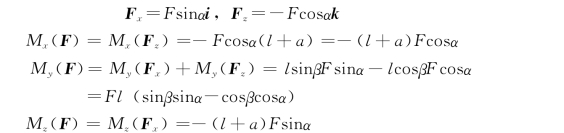
若利用式（3-9），并注意到Fy=0，则有

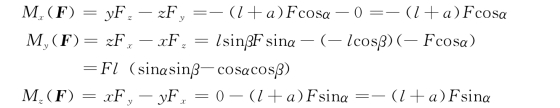
两种计算方法结果相同。