同平面力系一样,研究空间力系的简化、合成及平衡问题也需将力系中各力在空间坐标轴上进行投影。通过第二章的研究得知,力在某轴上的投影等于该力矢量与该轴单位矢量之数量积,现在可将其推广至空间力系中。
设有一力F作用于物体的O 点上,如图3-2 (a)所示,现过O 点作一空间坐标Oxyz,并以i、j、k分别表示Ox、Oy、Oz轴的单位矢量,若力F的方向角α、β、γ (力F与坐标轴Ox、Oy、Oz正向夹角)为已知,则根据力的投影定义,可得出该力在三个坐标轴上的投影分别为

式中:cosα、cosβ、cosγ为力F的方向余弦。
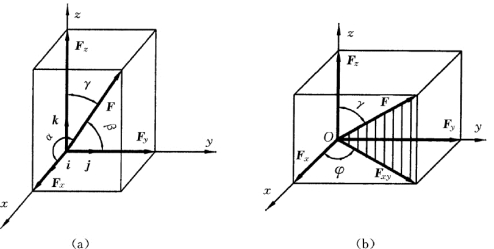
图3-2
当力F的方向角不能全部得知,但已知确定F方向的其他角度时,如图3-2 (b)所示,已知力F与z轴的夹角γ和F在Oxy面上的分力Fxy与Ox轴的夹角φ,则可先将力F分解为沿z轴和垂直于z轴两个分力Fz 和Fxy,然后再将此二分力分别向各坐标轴上投影得

在一些实际问题中,应用这个方法计算投影往往比较方便。这种投影法称为二次投影法。
从上面的分析不难看出,如果力F的大小和方向是已知的,则它在选定坐标系的三个轴上的投影是确定的(坐标系不定,投影则无法确定);反过来,若已知力F在选定坐标系的三个坐标轴上的投影Fx、Fy、Fz,则力F的大小及方向也随之唯一确定,这说明力和它在选定坐标轴上的投影具有一一对应的关系。对于正交坐标系,在已知力在各轴上投影的情况下,其力的大小为
![]()
其方向余弦为

从前面的分析还可以看出,对于正交坐标系,力在坐标轴上的投影Fx、Fy、Fz 和力沿坐标轴的分量的大小是相同的,在图3-2 (a)中,显然有(https://www.xing528.com)
![]()
由此可得力沿坐标轴的解析式
![]()
【例3-1】 在正方体的顶点A和B 处,分别作用力F1 和F2,如图3-3所示。试求此二力在x,y,z轴上的投影。
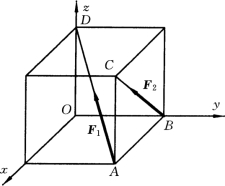
图3-3
解:设正立方体的边长为a,则
![]()
F1 在三个坐标轴上的投影为
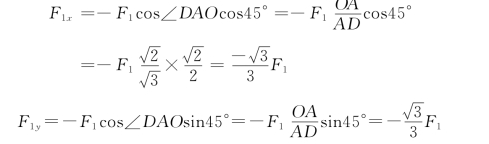
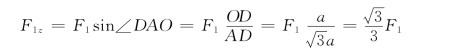
F2 在3个坐标轴上的投影
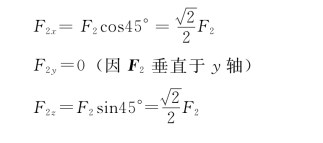
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




