平面力系平衡方程式的应用-理论力学

应用平衡方程式求解平衡问题的方法称为解析法，它是求解平衡问题的主要方法。这种解题方法包含以下步骤。

1．选取研究对象进行受力分析

所谓研究对象，是指为了解决问题而选择的分析主体。选取研究对象的原则是：要使所取物体上既包括已知条件，又包括待求的未知量。选取之后，要对它进行受力分析。画出受力图。

2．建立平衡方程式

这是解决问题的主要步骤。在这个步骤中，为了顺利地建立起平衡方程式，可采取以下三个步骤：

（1）根据所研究的力系选择平衡方程式的类别 （如汇交力系、平行力系、一般力系等）和形式（如基本式、二矩式、三矩式）。

（2）建立投影轴，列投影方程式。投影轴的选取原则是任意的，不一定非取水平或垂直方向，应根据具体问题从解题方便入手去考虑。

（3）取矩心，列力矩方程。矩心的选取也要从解题方便的角度加以考虑。

3．解平衡方程式求得其中的未知量

平衡方程式一般是一个线性方程组，这表明一个静力学的平衡问题经过上述力学分析之后将归结为一个线性方程组的求解问题。从理论上说，只要所建立的平衡方程组具有完整的定解条件，如独立方程个数与未知量个数相等，求解它是不困难的。但是如果所要解的方程组互相联立，则计算往往比较麻烦。为了避免这种麻烦，就要求在列平衡方程时运用一些技巧，使得所建立的各平衡方程式之间尽量相互独立，即每个方程中只含一个未知量，以方便求解。

【例2-2】 图2-19 （a）所示拖拉机的制动蹬，制动时用力F踩踏板，通过拉杆CD使拖拉机制动。设F=100N，踏板和拉杆自重不计，求图示位置拉杆的拉力FT 和铰链B处的支座反力。

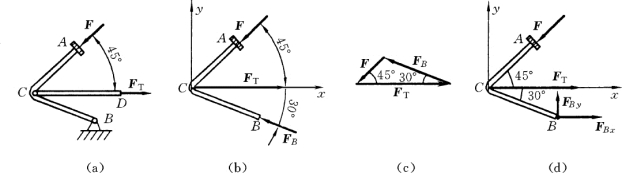
图2-19

解：（1）取研究对象，作受力图。

因为踏板ACB上既有已知力F，又有未知力FT和B处的约束反力，所以取ABC为研究对象。注意到ACB上受有F，FT和B处约束反力FB三个力作用而平衡，故可用三力平衡汇交定理确定FB的方向。至于FB的指向，可先假设，待计算之后根据FB 的正负号再判断其真实方向。

另外，拉杆CD是二力杆，按二力平衡公理可直接确定C端约束反力的方向，因此不必单独取拉杆CD作为研究对象。受力图如图2-19 （b）所示。

（2）列平衡方程式。

1）选择平衡方程的类型。由于ACB上受一个平面汇交力系作用，故应选用平面汇交力系的平衡方程，共有两个投影式，即式（2-22）。

2）选择投影轴如图2-19 （b）所示。

列方程

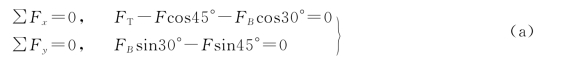
3）解方程组（a）得

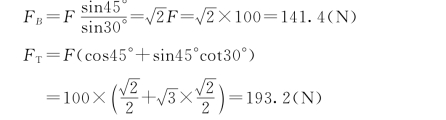
最后由计算结果知：FB 为正值，说明受力分析时假定的方向与实际方向一致。

分析讨论：

（1）本例中所研究的力系是由三个力组成的平面汇交力系。对于这样的问题，亦可采用几何法求解，即利用平面汇交力系平衡的几何条件，将三个力组成自行封闭、各力首尾相接的力三角形，并根据几何关系求得未知力FT 与FB。力三角形如图2 19 （c）所示。

根据正弦定理可以解出

及

按力三角形自行封闭的矢序规则，可确定出FB 的方向。

（2）若在受力分析中不利用三力平衡汇交定理，则B处约束反力亦可由一对正交分力FBx与FBy表示。这样踏板上所受的就是一个平面一般力系，于是需要选用平面一般力系的平衡方程，如基本式 （2-19）。选用坐标如图2-19 （d）所示，并以B点为矩心。

由式（b）可解得

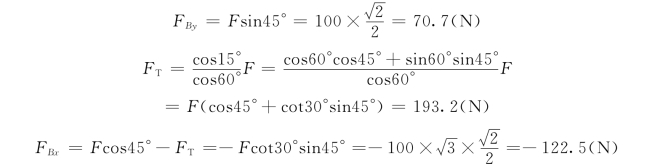
为了与前面的结果进行比较，可将FBx与FBy合成为FB，即

FB的方向可由角α表示

所以α=150°，与前面的结果一致。注意这里的α是力FB 与x轴正向之间的夹角。

由上述讨论可知：当物体在三个不平行的共面力作用下处于平衡时，用三力平衡汇交定理解题可使计算过程有所简化。

【例2-3】 铰车系统如图2-20 （a）所示，其中直杆AC和BC 铰接于C 点，自重不计。C处滑轮尺寸不计。重物P=20kN通过钢丝绳悬挂于滑轮上并与铰车相连。试求平衡时杆AC和BC所受的力。

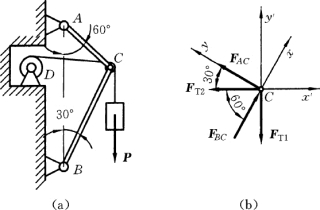
图2-20

解：由题意，滑轮尺寸不计，而AC和BC均为二力杆，因此本题中各个力都交于C点，构成一个平面汇交力系，可取销钉C作研究对象，其受力如图2-20 （b）所示。而且已知其中绳的张力均为P，即FT1=FT2=P。

对于平面汇交力系，应选用方程式（2-22），因此可以列出两个投影方程。注意到力系中的两个未知力FAC和FBC互相垂直，于是就按它们的方向取投影轴，从而得

(www.xing528.com)

在这里容易看到：由于坐标轴的方向刚好与其中一个未知力垂直，因此每个投影方程中只包含了一个未知量，很容易从中解得

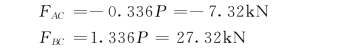
假如当初不这样选取投影轴，而是以水平方向和铅垂方向为投影轴，则得到的方程组将是一个联立的方程组，虽然也可以得未知反力FAC和FBC，但求解过程将比较繁琐。

另外在所得到的结果中，FAC是负值，表明其实际方向与假设的方向相反，即AC杆与BC杆一样，均受压力。

还需说明，本题虽然也是平面汇交力系问题，但却不宜用几何法求解，因为共有四个力，将构成一个不规则的四边形，几何法求解比较麻烦。因此，解析法比几何法实用性更强。

【例2-4】 塔式起重机如图2-21所示。其中机身重心位于C处，自重P1=800kN。起吊重力P2=300kN的重物，几何尺寸如图2-21所示，其中a=5m，b=3m，l=8m，e=1m。试求：

（1）为使起重机满载和空载时都不致翻倒，平衡配重P3应取何值？

（2）若取P3=500kN，则满载时导轨A和B 所受压力各为多少？

解：取整个起重机为研究对象，进行受力分析后得知，这是一个平面平行力系的问题。为使起重机不翻倒而始终处于平衡状态，主动力P1、P2、P3 和约束力FA、FB 必须满足平衡条件，即满足平面平行力系的平衡方程式（2-23）。

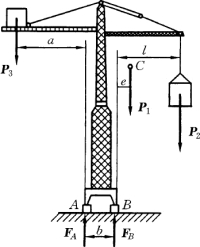
图2-21

（1）为使起重机不翻倒，应分别考虑满载和空载时起重机处于极限平衡状态的情况。

满载时，机身处于可能绕B点转动而翻倒的极限平衡状态。此时应有A支座处的约束反力FA=0，即A 轮与地面将要脱离接触。这时求出的平衡配重应为最小值，记为P3min。

应用平衡方程式（2-23），可求得此时的FB 及P3min，但据题意只求P3min，故只需列方程∑MB=0，即可求得P3min，而不必去求FB。

由∑MB=0得

解得

空载时，起重机可能绕A点向左翻倒。在这种极限平衡状态下，有B支座处约束反力FB=0，由此可求得平衡配重的最大值P3max。

由∑MA=0得

解得

于是为使起重机不致翻倒，平衡配重P3 应满足

（2）由题意知，P3=500kN，根据前面的计算，起重机可以保持平衡，为求FA 和FB，利用方程（2-23），以铅垂轴y为投影轴，并以A为矩心，于是有

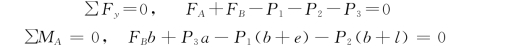
可解得

顺便指出，平面平行力系的平衡方程式也不是只有式 （2-23）惟一的形式，如本题（2）中亦可由方程式∑MA=0，∑MB=0求出FA 和FB。

【例2-5】 图2-22 （a）所示机构的自重不计。圆轮上的销子A放在摇杆BC 上的光滑导槽内。圆轮上作用一力偶，其力偶矩为M1=2kNm，OA=r=0．5m。图示位置时OA与OB 垂直，α=30°，且系统平衡。求作用于摇杆BC上力偶的矩M2 及铰链O、B处的约束反力。

解：先取圆轮为研究对象，其上受有矩为M1 的力偶及光滑导槽对销子A 的作用力FA 和铰链O 处约束反力FO 的作用。由于力偶必须由力偶来平衡，因而FO 与FA 必定组成一力偶，力偶矩方向与M1 相反，由此定出FA 指向如图2-22 （b）。而FO 与FA 等值且反向。由力偶平衡条件

解得

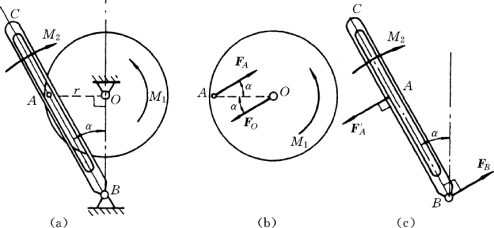
图2-22

再以摇杆BC为研究对象，其上作用有矩为M2 的力偶及力F′A 与FB，如图2-22（c）所示。同理F′A 与FB 必组成力偶，由平衡条件

其中F′A=FA。将式（a）代入式（b），得

FO 与FA 组成力偶，FB 与F′A 组成力偶，则有

方向如图2-22 （b）、（c）所示。