平面任意力系简化结果讨论

平面力系向作用面内一点简化后得到的主矢和主矩，进一步分析可能出现以下四种情况：

（1）F′R=0，MO≠0；

（2）F′R≠0，MO=0；

（3）F′R≠0，MO≠0；

（4）F′R=0，MO=0。

分别讨论这些情况，可以得到力系简化的最终结果和一些有用的结论。

（1）F′R=0，MO≠0：说明该力系无主矢，而最终简化为一个力偶，其力偶矩就等于力系的主矩。值得指出的是：当力系简化为一个力偶时，主矩将与简化中心的选取无关。

（2）F′R≠0，MO=0：说明原力系的简化结果是一个力，而且这个力的作用线恰好通过简化中心O点，这个力就是原力系的合力。在这种情况下，记F′R=FR，以将它与一般力系的主矢相区别。

（3）F′R≠0，MO≠0：这种情况还可以进一步简化。由力系平移定理知：F′R 与MO 可以由一个力FR 等效替换，这个力FR=F′R，但其作用线不通过简化中心O。若设合力作用线到简化中心O的距离为d，则

图2-13可说明上述简化过程，其中O′为合力FR 的作用点。

另外由图2-13 （b）及证明过程知

于是得合力矩定理：平面任意力系的合力对力系所在平面内任意点的矩等于力系中各力对同一点的矩的代数和。

（4）F′R=0，MO=0：说明该力系对刚体总的作用效果为零。根据牛顿惯性定理知，此时物体将处于静止或匀速直线运动状态，即物体处于平衡状态。

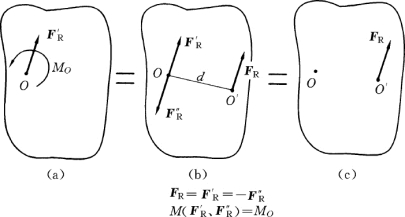
图2-13

【例2-1】 重力坝受力如图2-14所示，设P1= 450kN，P2=200kN，F1=300kN，F2=70kN。求力系的合力FR 的大小和方向余弦、合力与基线OA的交点到点O的距离x，以及合力作用线方程。

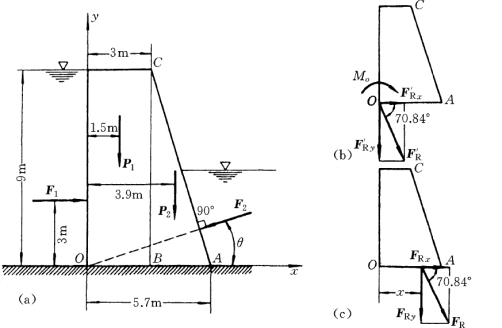
图2-14

解：（1）先将力系向点O简化，求得其主矢F′R 和主矩MO （图2-14b）。由图2-14（a）有

主矢F′R 在x、y轴上的投影为

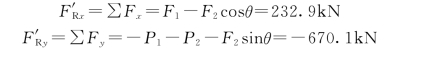(www.xing528.com)

主矢F′R 大小为

主矢F′R 的方向余弦为

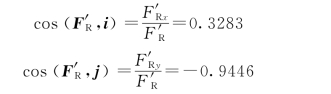
则有

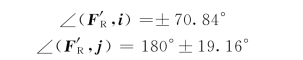
故主矢F′R 在第四象限内，与x轴的夹角为-70．84°。力系对点O的主矩为

（2）合力FR 的大小和方向与主矢F′R 相同。其作用线位置的x值可根据合力矩定理求得 [见图2-14 （c）]，即

其中

故

解得

（3）设合力作用线上任一点的坐标为 （x，y），将合力作用于此点，则合力为FR 对坐标原点的矩的解析表达式为

将已求得的MO、∑Fx、∑Fy 的代数值代入上式，得合力作用线方程为

即