平面任意力系的简化[理论力学]

设刚体上作用的n个力F1、F2、…、Fn 组成平面任意力系，如图2-10 （a）所示，在力系所在平面内任取点O作为简化中心，由力的平移定理将力系中各力矢量向O点平移，如图2-10 （b）所示，得到作用于简化中心O点的平面汇交力系F′1、F′2、…、F′n和附加平面力偶系，其矩为M1、M2、…、Mn。

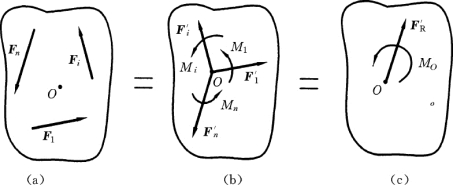
图2-10

平面汇交力系F′1、F′2、…、F′n可以合成为力的作用线通过简化中心O 的一个力F′R，此力称为原来力系的主矢，即主矢等于力系中各力的矢量和。有

平面力偶系M1、M2、…、Mn 可以合成一个力偶，其矩为MO，此力偶矩称为原来力系的主矩，即主矩等于力系中各力矢量对简化中心的矩的代数和。有

结论：平面任意力系向力系所在平面内任意点简化，得到一个力和一个力偶，如图2-10 （c）所示，此力称为原来力系的主矢，与简化中心的位置无关；此力偶矩称为原来力系的主矩，与简化中心的位置有关。因此在提到主矩时必须指明简化中心。

力系主矢的计算，可以根据力在轴上的投影及合力投影定理，直接由原始力系得出。即选定直角坐标系Oxy，计算出各力在两轴上的投影，再根据合力投影定理得到主矢在两轴上的投影，最后求得主矢的大小和方向为

主矩的解析表达式为(www.xing528.com)

作为平面任意力系简化的应用，在此介绍一种常用的约束——固定端 （插入端）约束。它是使被约束体插入约束体内部，被约束体一端与约束成为一体而完全固定，既不能移动也不能转动的一种约束形式。

工程中固定端约束是一种常见的约束。例如夹紧在刀架上的车刀，与刀架完全固定成为一体。车刀受到的约束就是固定端约束，如图2-11 （a）所示。

又如物体的一端自由，另一端插入墙壁，它所受到的约束也是固定端约束。这种物体称为悬臂梁，如图2-11 （b）所示。

固定端约束的约束反力是由约束与被约束体紧密接触而产生的一个分布力系。当外力为平面力系时，约束反力构成的这个分布力系也是平面力系。由于其中各个力的大小与方向均难以确定，因而可将该力系向A点简化，得到的主矢用一对正交分力FAx和FAy表示，而将主矩用一个反力偶矩MA 表示，这就是固定端的约束反力，如图2-12所示。

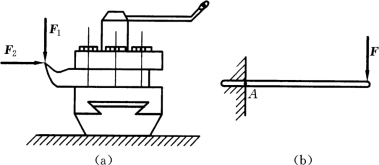
图2-11

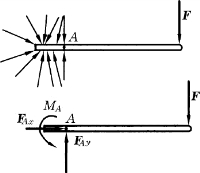
图2-12

特别需要指出的是：固定端约束与平面铰链约束中的固定铰链约束是有本质区别的，从约束效果上看，固定端约束既限制被约束体移动又限制其转动，而平面铰链约束则只限制被约束体移动，并不限制其转动；从约束反力的表示方法上看，固定端约束除与铰链约束一样，用一对正交分力表示约束反力的主矢之外，还必须加上一个约束反力偶，正是这个反力偶起着限制转动的作用。