【摘要】：如图2-2所示，若将力F沿直角坐标轴x和y分解得分力Fx 和Fy ，则力F在直角坐标系上投影绝对值与分力的大小相等，但应注意投影和分力是两种不同的量，不能混淆。图2-1图2-2图2-3力F在平面直角坐标系中的解析式为若已知力F在平面直角坐标轴上的投影Fx 和Fy，则力F的大小和方向为力既然是矢量，就满足矢量运算的一般规则。
设力F与轴x的夹角为α，如图2-1所示，力在坐标轴上的投影定义为力矢量F与x轴单位矢量i的标量积，记为
在力F所在的平面内建立直角坐标系Oxy，如图2-2所示，x和y轴的单位矢量为i、j，由力的投影定义，力F在x和y轴上的投影为
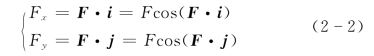
其中cos（F·i）、cos（F·j）分别是力F与坐标轴的单位矢量i、j的夹角的余弦称为方向余弦，（F·i）=α、（F·j）=β称为方向角。力的投影可推广到空间坐标系。
如图2-2所示，若将力F沿直角坐标轴x和y分解得分力Fx 和Fy ，则力F在直角坐标系上投影绝对值与分力的大小相等，但应注意投影和分力是两种不同的量，不能混淆。投影是代数量，对物体不产生运动效应；分力是矢量，能对物体产生运动效应；同时在斜坐标系中投影与分力的大小是不相等的，如图2-3所示。
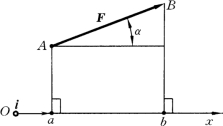
图2-1
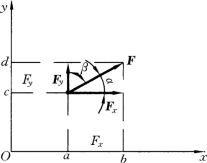
图2-2
(www.xing528.com)
图2-3
力F在平面直角坐标系中的解析式为
若已知力F在平面直角坐标轴上的投影Fx 和Fy，则力F的大小和方向为
力既然是矢量，就满足矢量运算的一般规则。根据合矢量投影规则，可得到一重要结论，即合力投影定理：合矢量在某一轴上的投影等于各分矢量在同一轴投影的代数和。
从而可得
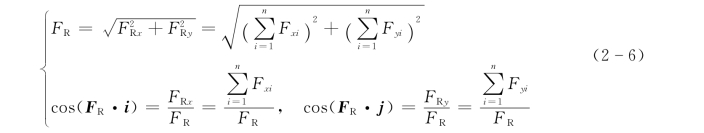
利用式（2-6），可以从原始力系出发，直接计算力系的合力以及主矢的大小和方向，这是很有意义的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
