第四节受力分析与受力图-理论力学成果提供

分析力学问题时，必须首先根据问题的性质、已知量和所要求的未知量，选择某一物体 （或几个物体组成的系统）作为研究对象，并假想地将所研究的物体从与之接触或连接的物体中分离出来，即解除其所受的约束而代之以相应的约束力，解除约束后的物体，称为隔离体。分析作用在隔离体上的全部主动力和约束力，画出隔离体的受力简图——受力图，这一过程即为受力分析。

受力分析是求解静力学和动力学问题的重要基础。具体步骤如下：

（1）选取研究对象并作出隔离体简图。

（2）画出所有作用在隔离体上的主动力（—般皆为已知力）。

（3）逐个分析约束，根据约束的性质画出约束力。

当选择若干个物体组成的系统作为研究对象时，作用于系统上的力可分为两类：系统外物体作用于系统内物体上的力，称为外力；系统内物体间的相互作用力称为内力。应该指出，内力和外力的区分不是绝对的，内力和外力只是相对于某一确定的研究对象才有意义。由于内力总是成对出现的，不会影响所选择研究对象的平衡状态，因此，在受力图上不必画出。此外，当所选择的研究对象不止一个时，要正确应用作用与反作用定律。确定相互联系的研究对象在同—约束处的约束反力应该大小相等。

【例1-1】 重力为P的圆球放在板AC与墙壁AB 之间，如图1-20 （a）所示。设板AC的重力不计，试作出板与球的受力图。

解：（1）先取球作为研究对象，画出简图。球上主动力有P，约束反力有FND和FNE，均属光滑面约束反力，所以为法向反力，受力图如图1-20 （b）所示。

（2）再取板作为研究对象。由于板的自重不计，故只有A、C、E′处有约束反力。其中A处为固定铰支座，其反力可用一对正交分力FAx和FAy表示；C处为柔性约束，其反力为拉力FT；E′处的反力为法向反力F′NE，要注意该反力与球在E处所受反力FNE为作用与反作用关系。受力图如图1-20 （c）所示。

另外，注意到板AC上只有A，E′，C处3个约束反力，并且处于平衡状态。因此可以利用三力平衡汇交定理确定出A处约束反力的方向，即先由力FT 与F′NE的作用线延长后求得汇交点O，再由点A向O点连线，则FA 的方向必沿着AO方向，受力图如1-20（d）所示。

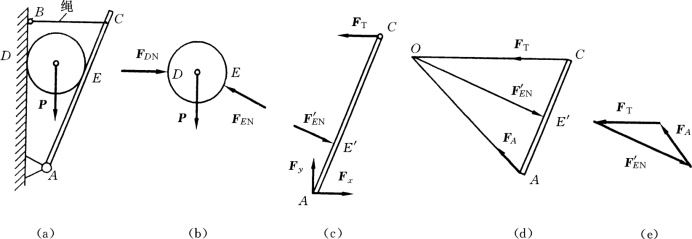
图1-20

至于FA 的指向，可以由平面汇交力系平衡的几何条件，即由力多边形自行封闭的矢序规则定出，其力多边形（在此例中为三角形）如图1-20 （e）所示。

【例1-2】 画出图1-21所示结构中各构件的受力图，不计各构件自重，所有约束处均为光滑约束。

解：当结构有中间铰时，受力图有两种画法。

（1）将中间铰单独取出。

这时将结构分为三部分：杆AB、铰B、杆BC。其中杆AB、BC都是二力杆，所以杆两端的约束力均沿杆端的连线，铰B处除受主动力F作用外，还受杆AB、BC在B 处的反力F′B1和F′B2的作用，如图1-21 （b）所示。

注意这里所说的二力构件，是指只受两个力作用而平衡的构件。在实际结构中，有些构件上不计自重，又无其他主动力作用，只在两处受有光滑铰链约束。这样的构件都是二力构件。对于这类构件，根据二力平衡条件，无论该构件形状如何，所受约束如何，只要将两个力沿作用点连线方向并相对反向画出即可。

（2）将中间铰置于任意一杆上。(www.xing528.com)

例如将中间铰B固连在杆AB 上，结构分为杆AB （带铰B）、杆BC两部分，受力分析结果如图1-21 （c）所示。

（3）本例讨论。

分析杆AB （带铰B），中间铰B固连在杆AB 上，铰B与杆AB 组成一个子系统，铰B与杆AB 的相互作用力FB1、F′B1成为系统内力，不用画出；在B点要画出的是主动力F和杆BC对铰B 的约束力F′B2（即系统外力）。若中间铰B固连在杆BC 上，请读者自己分析其受力。

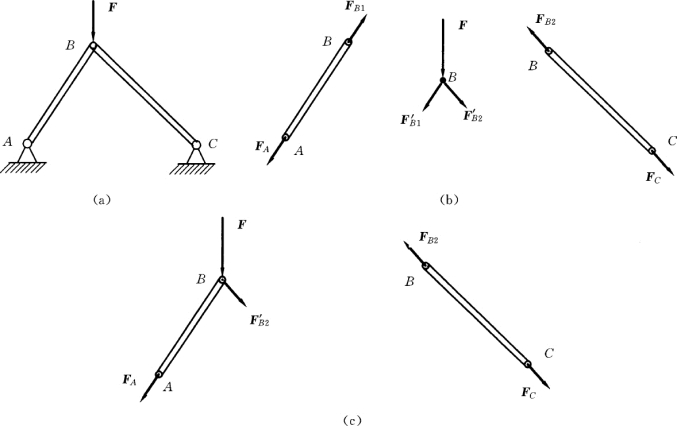
图1-21

【例1-3】 作图1-22 （a）所示三铰拱中两个构件的受力图。各构件自重不计。

解：（1）首先分析AC构件，由于不计拱的自重，AC构件是一个二力构件，因此先作它的受力图，如图1-22 （b）所示。

（2）取拱BC为研究对象，其上有主动力F，C处铰链的约束反力方向已由AC 部分定出；B处固定铰链的约束反力可由一对正交分力表示，如图1-22 （c）所示；也可由三力平衡汇交定理确定FB 的方向，如图1-22 （d）所示。

（3）需要说明的是：在上述分析过程中，C处用以连接两个构件的销钉，并没有单独被取作研究对象，因为销钉的受力分析一般用处不大，故可以把它带在某个构件上一起取作研究对象，通常亦无需指明销钉带在哪个构件上。在上面的分析中认为销钉在AC或BC上都可以。如果有必要指明销钉是在哪个构件上，可以在那个构件的C处表示铰链孔的圆圈内打一个点，如图1-22 （e）所示，表示销钉带在AC上。倘若有必要，还可以把销钉也单独取作研究对象。这时的受力图如图1-22 （f）所示。

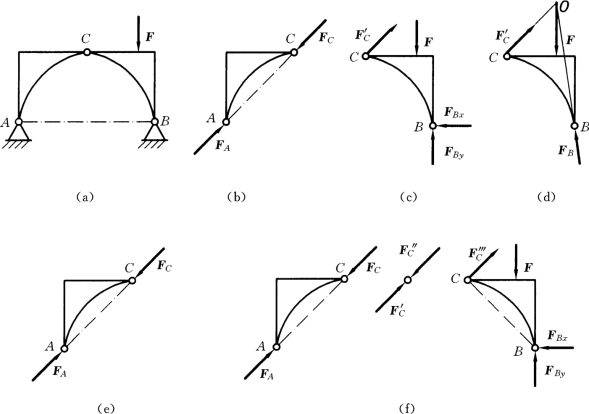
图1-22

下面一例为综合练习受力图的作法。

【例1-4】 图1-23所示的结构，不计各杆及滑轮的自重，试画出整体和各杆及滑轮的受力图。

解：先画整体受力图，如图1-23 （a）所示。

注意到结构中杆BC为二力杆，先作出其受力图，如图1-23 （b）所示。滑轮的受力图如图1-23 （c）所示。

杆CDE的受力图如图1-23 （d）所示，杆ADB的受力图如图1-23 （e）所示，注意其中C、D、E各点处的作用力与反作用力的关系。

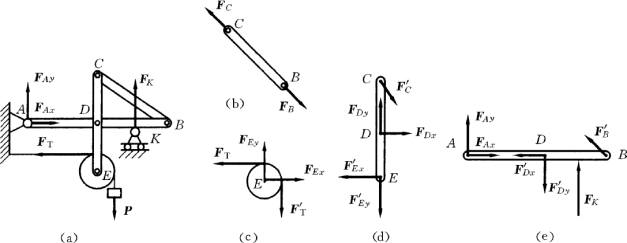
图1-23