混合同步系统复杂度分析：一项混沌同步研究

一个有限长度序列的复杂度是指它与随机序列的相似程度，是对利用序列的部分恢复出整体的难易程度的度量。因此，它是衡量一个伪随机序列复杂性和随机性的重要指标。目前，多数研究主要利用线性复杂度分析方法来判断伪随机序列的复杂度大小，但由于混沌伪随机序列是通过混沌系统迭代并由其演化轨迹得到，该方法并不能完全确定混沌伪随机序列的复杂性。

为了确定混沌伪随机序列的复杂度，必须从混沌系统本身的特征入手。由于混沌系统的相邻轨道是以指数速度分离的，在一定时间内可以区分的不同的轨道数目M越多，复杂度就越大。对于一个混沌运动轨道，随着时间的推移，M呈指数增长趋势，即

M∝eKt

其中，常数K是测度熵，它反映了混沌运动产生的速率。当产生的运动为规则运动时，K＝0；当产生的运动为纯随机运动时K＝＋∞；当产生的运动为混沌运动，0＜K＜＋∞。因此，常数K的值越大，随机性越强，被恢复的可能性越小，复杂度也就越高。

近似熵（Approximate Entropy，简写为ApEn）方法是一种有效计算测度熵的方法，理论和实验证明，ApEn可以通过较短的观察序列，有效计算混沌序列的测度熵，从而判断混沌伪随机序列的复杂度。本文采用近似熵ApEn来计算实现混合同步的耦合系统（2.1－8）～（2.2－1）的复杂度，用混沌轨道分离的速度大小来度量混沌伪随机序列的复杂度，ApEn的值越大，混沌系统的复杂度越高。

设耦合系统（2.1－8）～（2.2－1）实现混合同步后产生的时间序列为x（1），x（2），…，x（N）（截取的长度为N），则近似熵ApEn的值可以通过以下步骤计算得到：

（1）将序列｛x（i）｝按一定的顺序组成m维向量O（i），即

O（i）＝［x（i），x（i＋1），…，x（i＋m－1）］（i＝1，2，…，N－m＋1）

（2）定义m维向量O（i）和O（j）之间的最大距离

（3）将与第i个m维向量O（i）的最大距离小于r的向量数定义为(www.xing528.com)

（4）定义Φm（r）为

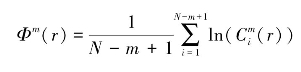
（5）此时间序列的近似熵定义为

参数m是距离向量的维数，公式（6.3－1）实际是计算在已知m个样本的情况下，产生第m＋1个样本的条件概率。近似熵ApEn的值显然与m和r的值有关，向量维数m的最大值由时间序列的长度N决定，当m越大时，ApEn越接近测度熵。距离参数r决定了计算过程的分辨率，r的值越小，ApEn的分辨率越高。根据经验，嵌入维数m通常取2，距离参数可以取r＝ad（x），其中，d（x）为产生的时间序列的标准差，a的取值范围为0.1≤a≤0.25。

对单一混沌系统（2.1－8）和耦合混沌同步系统（2.1－8）～（2.2－1），采用同样的初始值，分别计算二者所产生的时间序列的ApEn，计算结果如表6.4所示。其中，各参数取值为m＝2，a＝0.15，N＝5 000。

表6.4　时间序列的ApEn复杂度

表6.4给出了单一混沌系统和耦合同步系统在x、y和z3个维度的ApEn复杂度的值。通过数值计算得出，混合同步系统的复杂度比单一混沌系统平均高11%左右，应用混合同步系统产生的时间序列对图像进行加密的安全性会更高。