混沌同步在图像加密中的应用研究成果及安全性分析

为了验证基于三维猫映射的图像加密算法的有效性，分别对Lena灰度图像（大小为256×256）和一个普通文本图像进行加密。在本节的仿真实验中，混沌系统的初始值、参数和密钥设为：Hénon的初始值选为x0＝0.02和y0＝0.1，参数取为p＝1.4，产生置乱控制参数过程的3个密钥取值为r＝1000，t＝3000和k1＝12。Logistic映射的初始值选取为x0＝0.2和y0＝0.3，参数取为μ1＝3，γ1＝0.2，μ2＝3和γ2＝0.14。加密的结果如图6.2所示。

图6.2的实验结果表明，基于三维猫映射的图像加密算法在加密灰度图像和文本图像时都具有很好的加密效果。经过三维猫映射中的位置置乱和像素值替代，无论是纹理比较复杂的Lena图像，还是灰度值较少的文本图像，密文图像都变得完全无法识别。下面对加密算法的安全性作进一步的分析。

6.1.3.1　密钥空间分析

为了抵抗密钥的穷举攻击，加密算法应该具有尽可能大的密钥空间。在基于三维猫映射的图像加密算法中，先后使用到的4个初始值和3个控制参数都可以作为算法的密钥。4个初始值分别为Hénon映射和Logistic映射的初始值，3个控制参数为产生置乱控制参数使用到的r、t和k1。这些值的微小改变，都会导致混沌序列发生非常巨大的变化。如果每个初始值精确到小数点后14位，7个密钥构成的密钥空间大于2100。Alvarez和Li在相关文献中指出，只要密钥空间达到2100，加密算法就能够达到足够的安全级别抵御穷举破解法，因此，该加密算法提供了足够的密钥空间。

图6.2　Lena图像和文本图像的加密结果

（a）原始Lena图像　（b）Lena图像的密文图像　（c）文本图像　（d）文本图像的密文图像

6.1.3.2　密钥敏感性测试

一个好的加密算法应该对密钥非常敏感，这包括对加密过程敏感和对解密过程敏感两个方面。也就是说，对图像进行加密操作时，密钥微小的改变将导致完全不同的两个密文图像，对密文图像进行解密时，密钥微小的改变将导致解密结果完全不正确。

（1）加密过程敏感性测试

为了验证密钥对加密过程的敏感性，对大小为256×256的灰度Lena图像进行如下四组测试：

测试1.改变Hénon映射的第一个初始值为x0＝x0＋10－4；

测试2.改变Logistic映射的第二个初始值为y0＝y0＋10－4；

测试3.将控制参数的值调整为r＝r＋1；

测试4.将控制参数k1的值调整为k1＝k1＋1。

以上4个测试中密钥变化前后得到的密文图像的差异如表6.1所示。可以看出加密算法对密钥非常敏感，密钥很小的变化将会得到完全不同的密文图像，使得攻击者很难获得正确的明文图像。

表6.1　密文图像之间的百分比差异

（2）解密过程敏感性测试

图6.3给出了该加密算法在解密过程中对Hénon映射的初始值x0和t的敏感性测试结果。图6.3（a）为原始Lena图像，加密密钥x0＝0.02和t＝3000时的密文图像如图6.3（b）所示，当解密密钥取x0＝0.020 000 000 000 000 1，其他密钥正确时，错误的解密图像如图6.3（c）所示。当解密密钥取3001，其他密钥正确时，解密图像如图6.3（d）所示。可以看出，即使解密密钥x0的取值与加密密钥只相差10－14，我们将得到完全不正确的解密图像；当密钥t的取值只改变1时，得到的迭代次数n与实际值将会有很大差异，同样导致解密结果不正确。

图6.3　解密过程对密钥x0和t的敏感性

（a）原始图像　（b）密文图像（x0＝0.02，t＝3000）　（c）x0＝0.020 000 000 000 000 1得到的解密图像　（d）t＝3001得到的解密图像

以上测试结果表明，基于三维猫映射的图像加密算法对加密过程和解密过程都具有很强的敏感性，基本能够抵抗选择明文攻击和唯密文攻击。

6.1.3.3　统计分析

加密算法抵抗统计分析攻击的能力是判断加密算法是否安全的一个重要标准。本节从密文图像的灰度分布、密文图像的相关性和置乱过程的不动点等角度分析所提加密算法抵抗统计分析攻击的能力。

（1）密文图像的灰度分布

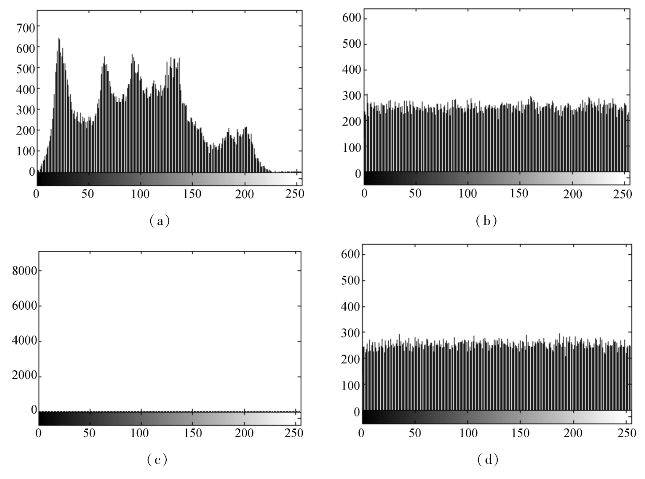
灰度分布是密码学中一个非常重要的特征，如果一个密文图像的灰度分布不均匀，将很容易被密文攻击所破解。图像的直方图能够直观地表现出图像的灰度分布情况，是图像中灰度值密度函数的近似表示。图6.4给出了图6.2中所有明文图像和密文图像的直方图。

(www.xing528.com)

图6.4　图6.2中明文图像和密文图像的直方图

（a）明文Lena图像的直方图　（b）密文Lena图像的直方图　（c）明文文本图像的直方图　（d）密文文本图像的直方图

可以看出，尽管明文图像的灰度分布非常不均匀，尤其是文本图像，它的灰度分布主要集中在0和255这两个像素值上，经过加密处理后，密文图像的灰度分布都变得很均匀，原始图像的统计特性完全发生了变化。

为了进一步验证密文图像的统计特性，计算密文图像像素的平均值和标准差。采用的3组测试图像如图6.5所示，其中，图6.5（a）是一个纹理比较复杂的灰度图像，图6.5（b）是一个灰度值较少的文本图像，图6.5（c）是一个只在中间位置有一个黑点的简单图像，相应的明文图像和密文图像和平均值和标准差计算结果如表6.2所示。

图6.5　测试图像

从表6.2可以看出，无论明文图像的灰度如何分布，经过加密算法加密后，所有图像像素的平均值都在128左右，标准差都在73左右。因此，攻击者如果只知道密文图像，很难根据图像的统计特性推断明文图像。

表6.2　图6.5中明文图像及密文图像的平均值和标准差

（2）相关性分析

明文图像中相邻像素的相关性通常是很大的，有效的图像加密算法应该能够尽可能低降低这种相关性，理想情况下应该能达到随机图像的相关性。为了测试图像中相邻像素之间的关系，本节引入相关系数rxy的概念，计算公式如下：

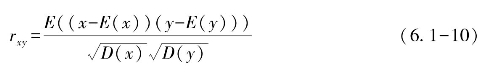
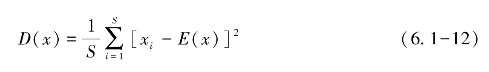
其中，x和y分别为两个相邻像素的像素值，E（x）为x的均值，D（x）为x的方差，整数S为测试像素点的数量。计算明文图像、密文图像和随机图像的相关系数rxy。

为了对基于扩展的三维猫映射的图像加密算法的相关性进行分析，分别针对原始Lena图像、本节算法加密的密文图像和随机图像，使用公式（6.1－10）～（6.1－12）计算每个图像M×N／2对像素点在水平方向、垂直方向和对角方向相邻像素的相关系数，计算结果如表6.3所示。可以看出，该加密算法能够极大地降低相邻像素之间的相关性。

表6.3　相邻像素相关系数的比较

本节仍然选取原始图像和加密图像的2 000个像素点，并分析这些点与水平方向、垂直方向和对角方向相邻像素点之间的相关性，相关性分析的散点图如图6.6所示。

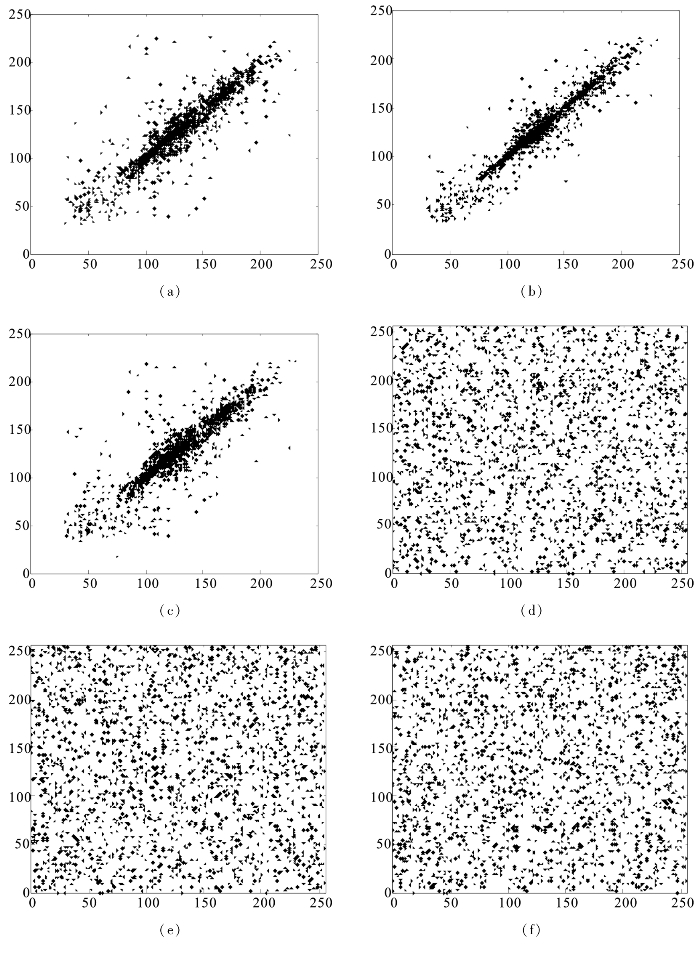
图6.6　相关性分析的散点图

（a）明文水平方向散点图　（b）明文垂直方向散点图　（c）明文对角方向散点图　（d）密文水平方向散点图　（e）密文垂直方向散点图　（f）密文对角方向散点图

从图6.6可以看出，原始Lena图像在水平方向、垂直方向和对角方向的相关性都很大，密文图像在这些方向的相邻像素相关性大大减小，基本具有抵御统计分析攻击的能力。

（3）置乱中的不动点

置乱中的不动点是指置乱操作后像素位置不发生变化的点。不动点的数目越少，置乱移动的点就越多，将会获得更好的加密效果。因此，最好的置乱效果是保证所有像素的位置都发生变化。为了验证所提加密算法的扩散性，对图6.7（a）中只包含一个黑点的简单图像进行置乱处理，处理结果如图6.7（b）所示。

图6.7　置乱中的不动点测试

（a）原始图像　（b）置乱图像

从图6.7可以看出，对于位于图像中间位置的黑点，置乱算法能够非常均匀地将图像中的黑色像素扩散到整个图像，几乎所有的像素都发生了位置的变化。