混沌同步仿真及其应用研究

公式（5.2－14）和公式（5.2－15）又称为Kalman滤波器方程，由此可得到Kalman滤波器的构造图，如图5.11所示。图5.11中，滤波器的输入是系统状态的观测值，输出是系统状态的估计值。

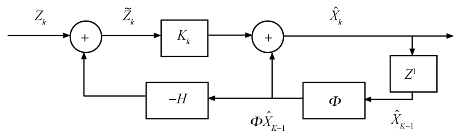
图5.11　Kalman滤波器框图

广义Kalman滤波基本方程，即公式（5.2－14）～公式（5.2－18）给出的滤波算法可由图5.12表示。图5.12描述了Kalman滤波的两个计算回路：增益计算回路和滤波计算回路。其中增益计算回路是独立计算的，而滤波计算回路依赖于增益计算回路。

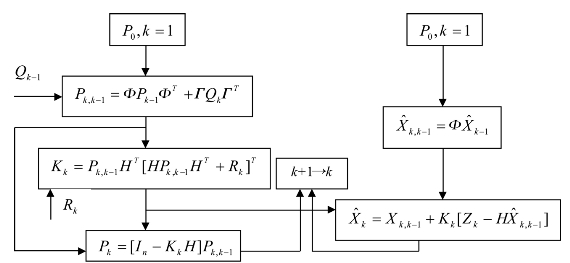
图5.12　Kalman滤波算法方框图

空间变换方法采用Kalman滤波作为空间变换形式。根据图5.12所示的Kalman滤波算法，可编写相应的Matlab程序。为了达到比较理想的同步状态，程序中各参数矩阵通过实验可以设为

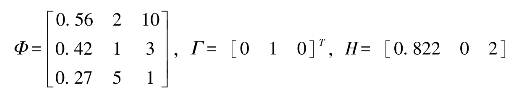
设定驱动系统初值为x0＝［0　0　1e－3］T，Wk和Vk为限幅噪声。

5.2.3.1　Lorenz系统方程与仿真

仿真实验中，选取Lorenz方程作为原系统，其方程为

公式（5.2－19）中，a、b、c均为系统参数。当系统参数a＝8／3，b＝10，c＝28时，Lorenz系统有一个混沌吸引子，即系统处于混沌状态。以Kalman滤波器作为空间变换函数对这一混沌吸引子进行影射变换。其中，抽取Lorenz系统各状态轨迹2 000个离散点，并对原系统与变换后的系统各分量进行比较，结果如图5.13～图5.16所示。

图5.13为Lorenz驱动系统与响应系统吸引子。

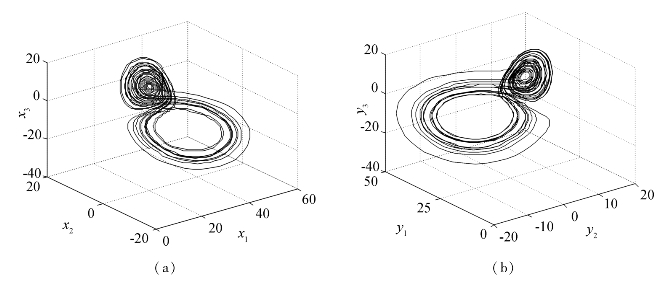
图5.13　Lorenz驱动与响应系统吸引子

（a）驱动系统吸引子　（b）响应系统吸引子

图5.14为Lorenz系统原空间分量x1与新空间分量y1比较图。

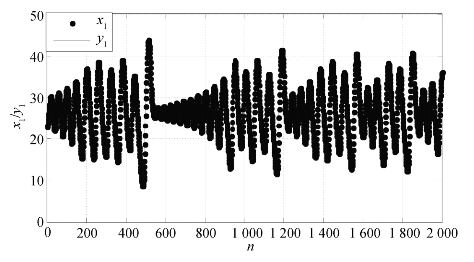
图5.14　Lorenz原空间分量x1与新空间分量y1比较

图5.15为Lorenz系统原空间分量x2与新空间分量y2的比较图。

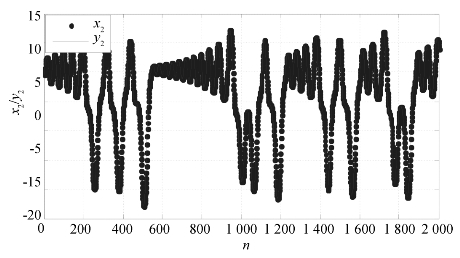
图5.15　Lorenz原空间分量x2与新空间分量y2比较

图5.16为Lorenz系统原空间分量x3与新空间分量y3的比较图。(www.xing528.com)

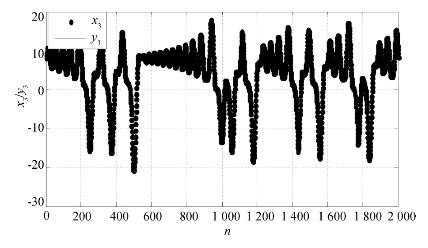
图5.16　Lorenz原空间分量x3与新空间分量y3比较

从图5.13可知，Lorenz系统的原混沌吸引子经过Kalman滤波变换，影射到了另一个新的空间中，且在新空间中的混沌吸引子形状与其在原空间中的形状基本一致。更具体地，图5.14～5.16表示了Lorenz系统吸引子在新空间的分量与原空间的分量在上升、下降、平移等动力学性质上保持一致，只有具体数值有细微差别。由此可知，此时驱动系统与影射系统达到广义同步。

5.2.3.2　Rössler系统方程与仿真

选用Rössler系统方程作为原系统

公式（5.2－20）中，a、b、c均为系统参数。当a＝0.45，b＝2，c＝4时，系统呈现混沌状态。以同样方法进行变换，抽取Rössler系统各状态轨迹1 000个离散点，采用三维画图方法还原原系统，并对原系统与变换后的系统各分量进行比较，结果如图5.17～图5.20所示。

图5.17为Rössler驱动系统与响应系统的吸引子。

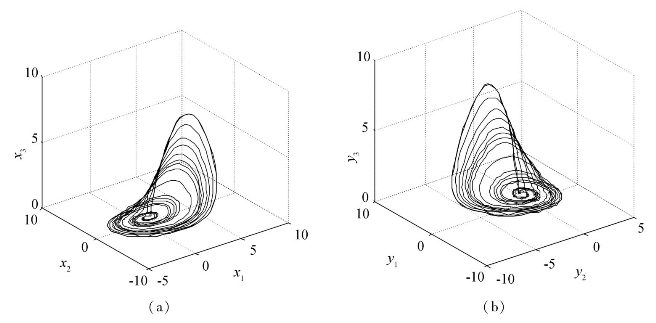
图5.17　Rössler驱动与响应系统吸引子

（a）驱动系统吸引子　（b）响应系统吸引子

图5.18为Rössler系统原空间分量x1与新空间分量y1的比较图。

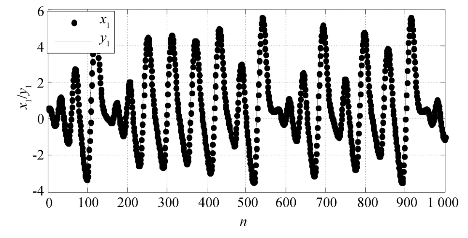
图5.18　Rössler原空间分量x1与新空间分量y1比较

图5.19为Rössler系统原空间分量x2与新空间分量y2的比较图。

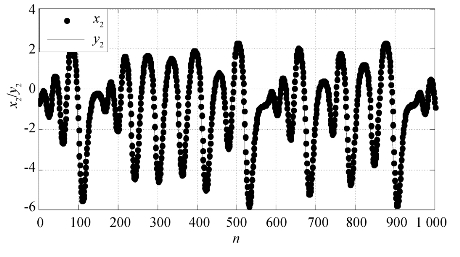
图5.19　Rössler原空间分量x2与新空间分量y2比较

图5.20为Rössler系统原空间分量x3与新空间分量y3的比较图。

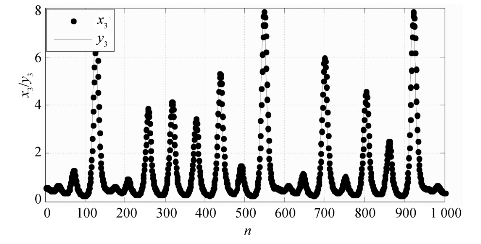
图5.20　Rössler原空间分量x3与新空间分量y3比较

从图5.17可知，Rössler系统的原混沌吸引子经过Kalman滤波变换，影射到了另一个新的空间中，且在新空间中的混沌吸引子形状与其在原空间中的形状基本一致。更具体地，图5.18～图5.20表示了Rössler系统吸引子在新空间的分量与原空间的分量在上升、下降、平移等动力学性质上保持一致，只有具体数值有细微差别。由此可知，此时驱动系统与影射系统达到广义同步。

由图5.13～图5.20可得，利用Kalman滤波变换方法分别把Lorenz混沌系统和Rössler混沌系统影射到新的空间。通过仿真实验，图5.13和图5.17分别得到两混沌系统原吸引子与新吸引子的三维立体图形，可以看出它们具有几乎一致的形状。图5.14～图5.16和图5.18～图5.20的实验结果表明，通过分析两混沌系统变换前后各维对应分量的动力学性质可知，它们的驱动系统与影射系统都达到广义同步。