系统广义同步速度改善：基于混沌同步新方法

研究表明，当满足矩阵（A－BK）稳定和矩阵（A，B）可控两个条件时，通过选择不同的矩阵B、K，可以改变其极点位置，从而使广义同步速度得到改善。同理，在确定B值的前提下，通过为矩阵（A－BK）选取不同的极点位置，得到不同的增益矩阵K，可以得到较好的广义同步速度。在工程中同样可以通过选择适当的极点，使系统广义同步速度得到改善。

5.1.4.1　Lorenz系统广义同步速度的改善

在Lorenz系统中，对照图5.5（a）所给条件，同样设

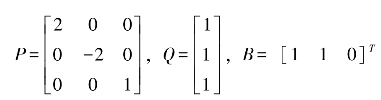
系数矩阵。分别取不同极点J值，再次调用Matlab软件中的place函数，得到增益矩阵K的值。

当Lorenz系统选取极点J＝［－10　－0.4＋0.3i　－0.4－0.3i］T时，得到K1＝［－1.104 94　－1.817 2　9.475 2］；若选取极点J＝［－30　－3＋0.4i　－3－0.4i］T时，K2＝［－1.192 3　23.525 6　13.578 8］。此时，广义同步误差e＝［e1　e2　e3］T的仿真曲线分别如图5.6和5.7所示。

图5.6为Lorenz系统中速度改善后极点选为K1时的广义同步误差曲线。

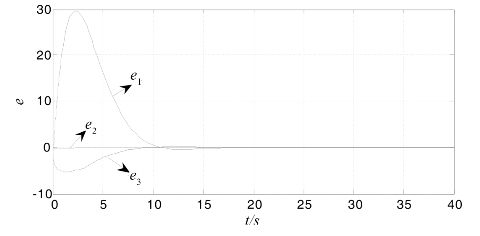
图5.6　Lorenz系统中速度改善后极点K1的广义同步误差曲线

图5.7为Lorenz系统中速度改善后极点选为K2时的广义同步误差曲线。

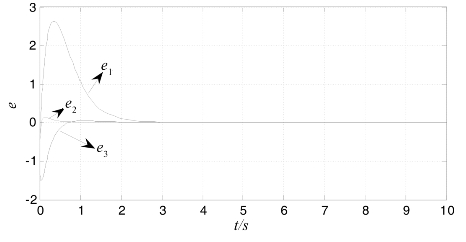
图5.7　Lorenz系统中速度改善后极点K2的广义同步误差曲线

由图5.6和图5.7可得，不同极点J对系统同步速度具有较大的影响。图5.6的系统同步时间大约为20 s，图5.7的系统同步时间大约为4 s。为了对Lorenz系统极点与同步速度之间的关系有更深的认识，表5.1列出了不同极点J及对应的混沌广义同步时间t。

表5.1　极点与广义同步时间的关系

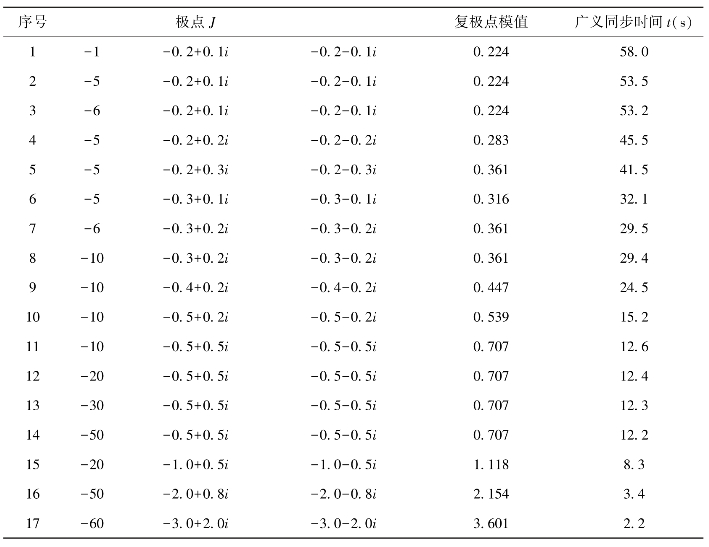
由表5.1可以看出，极点J的变化会导致不同的广义同步时间。随着复极点模值的增大，同步时间在逐渐减小。然而，由于复极点实部与虚部对同步时间的影响不同，会有个别幅值小但同步时间小的情况发生。如表5.1中第6个极点与同步时间所示，取极点J＝［－5　－0.3＋0.1i　－0.3－0.1i］T时，模值为0.316，其同步时间为32.1 s。极点对广义同步时间的具体影响，将在5.1.4.3节详细讨论。

5.1.4.2　LC振子系统广义同步速度的改善

在LC振子系统中，对照图5.5（b）所给条件，同理取

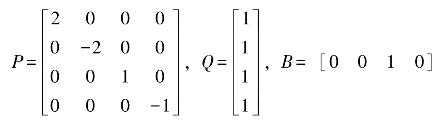
系数矩阵，满足构造条件。

当LC振子系统选取极点J＝［－20　－10　－0.3＋0.4i　－0.3－0.4i］T，得到增益矩阵K1＝［－191.307 6　－137.795 5　31.500 0　14.035 1］；同理，若LC振子系统选取极点J＝［－50　－30　－2＋0.3i　－2－0.3i］T时，则可得到增益矩阵K的值为K2＝104×［0.455 7　－1.260 9　0.008 5　0.212 8］。系统广义同步误差e＝［e1　e2　e3　e4］T的仿真曲线如图5.8和图5.9所示。(www.xing528.com)

图5.8为LC系统中速度改善后极点选为K1时的广义同步误差曲线。

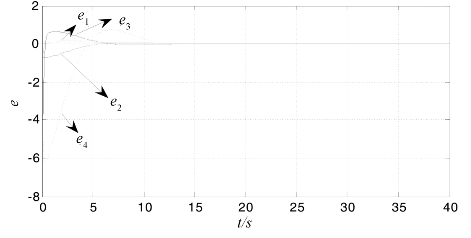
图5.8　LC系统中速度改善后极点K1的广义同步误差曲线

图5.9为LC系统中速度改善后极点选为K2时的广义同步误差曲线。

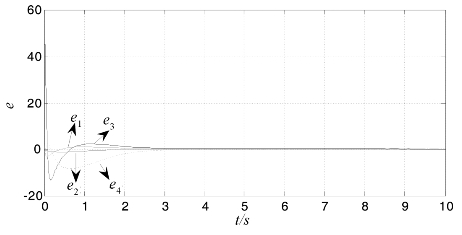
图5.9　LC系统中速度改善后极点K2的广义同步误差曲线

由图5.8和图5.9可知，采用不同极点J时，系统达到同步的时间各异。图5.8的系统同步时间大约为20 s，图5.9的系统同步时间大约为5 s。为了对LC振子系统的极点与同步速度之间的关系有更深的认识，表5.2列出了不同极点J及对应的混沌广义同步时间t。

表5.2　极点与广义同步时间的关系

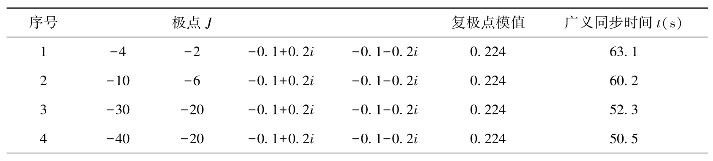
续表

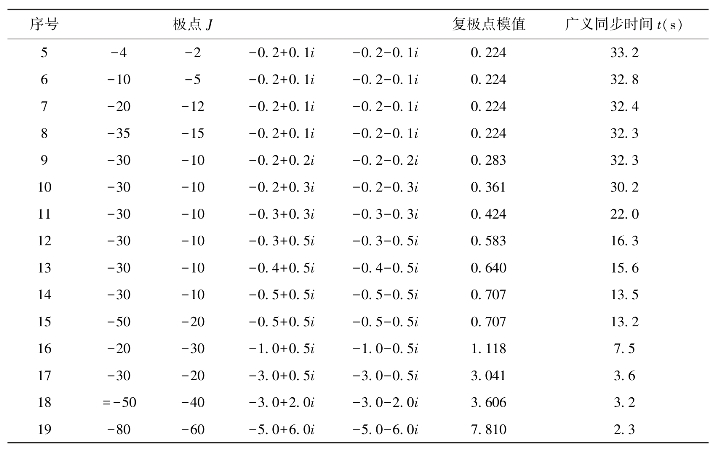
同理，由表5.2可知，极点J的变化会产生不同的广义同步时间。极点对广义同步时间的具体影响，将在5.1.4.3节详细讨论。

5.1.4.3　极点配置对广义同步速度的影响

由图5.6～图5.9以及表5.1和表5.2可知，不论是Lorenz系统还是LC振子系统，极点配置对广义同步速度的影响主要有以下4个特点：

（1）当矩阵B值确定时，（A－BK）的极点位置越远离原点位置，则系统广义同步的时间越短，达到同步的速度越快。反之同步时间越长，达到同步的速度越慢。

（2）对于不同极点J，若其复极点相同，选取不同的实极点对系统同步速度的影响较小。随着实极点离原点的距离增大，系统同步速度加快，系统达到同步的时间减少，同步性能得到改善。

（3）对于不同极点J，当其实极点相同时，采用不用的复极点对系统同步速度的影响较大。同样随着复极点离原点的距离增大，系统同步速度加快，系统达到同步的时间减少，同步性能得到改善。

（4）极点J具有相同实极点时，复极点的实部与虚部对系统同步速度的影响大小不同。实部对系统同步速度影响较大，虚部影响较小。两者都随着与原点的距离增大，系统同步速度加快。

此外，当Lorenz系统与LC振子系统选取相同主导复极点时，LC振子系统达到同步的时间比Lorenz系统达到同步的时间更短。而且，在两个系统的极点变化幅度一致时，LC振子系统的同步性能比Lorenz系统的同步性能改善的幅度大，同步时间递减得更快。