混沌同步仿真的应用研究成果

仿真技术是随着时间数值的增加，一步一步地求解系统动态模型方程的方法。仿真过程中，任何一步计算所得的即时值，都表示在指定时间内已被模型化了的系统状态。这样，在全部时间内就可以通过对系统的动态模型性能的观测来求得问题的解。系统仿真技术广泛应用于航空、空间、核能及工业过程控制等诸多领域，以进行系统分析、系统设计、系统测试、系统功能实验及操作训练等，近年来仿真技术又被广泛推广，应用于社会、经济、生物等非工程领域，用以进行系统的预测及运筹控制的研究。

对于从理论上构造和证明了的模型（5.1－13），其构造方法的有效性和可行性还需要进一步验证。为此，选取Lorenz混沌系统和LC振子系统分别进行数值仿真，验证此构造方法的有效性以及应用于高维系统的可行性。

5.1.3.1　Lorenz方程及其仿真系统设计

Lorenz混沌系统的动力学模型为

公式（5.1－14）中，a、b、c均为系统参数。当系统参数a＝8／3，b＝10，c＝28时，Lorenz系统有一个混沌吸引子，即系统处于混沌状态。

按照公式（5.1－12），将公式（5.1－14）分解成线性部分和非线性部分，同时引入可调参数β，得到线性系数矩阵A及其对应的非线性函数Φ（x）为：

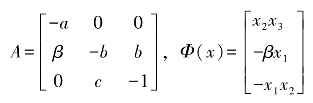
可调参数β的引入改变了系数矩阵A为常系数矩阵的性质，调整了驱动系统对响应系统的驱动函数Φ（x），加强了两系统之间的耦合关系。其次，可调参数β的引入并不改变驱动系统的状态方程和动力学行为，在同一极点上，通过对参数β的调节可以实现响应系统与驱动系统的最佳同步。因此，可以通过选取不同的可调参数β来构造不同的系数矩阵A及其对应的非线性函数Φ（x）。

不失一般性，选择

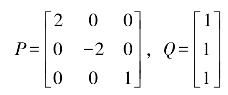
容易验证P为满秩矩阵，Q为常系数矩阵。

设参数β＝－1，则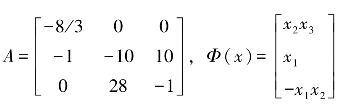。另外，为了使（A，B）可控，任取B＝［1　1　0］T满足rank（ctrb（A，B））＝3。

根据模型（5.1－13），极点的选择采用一对主导复极点和一个实极点，例如：

J＝［－3　－0.2＋0.1i　－0.2－0.1i］T

增益向量K值采用Matlab中的place函数来确定。依照以上所给A、B、J值，可得K＝［－1.010 1　－9.256 6　9.918 3］。任取公式（5.1－14）系统初值为x0＝［0　0　0.001］T，则根据公式（5.1－13）构造的响应系统初值为y0＝［0　0.001　0］T。该系统广义同步误差为e＝［e1　e2　e3］T，是三维向量。按照上述设定的值，利用Matlab7.1中的Simulink模块构建仿真系统，图5.1是构造的Lorenz方程仿真系统模型。

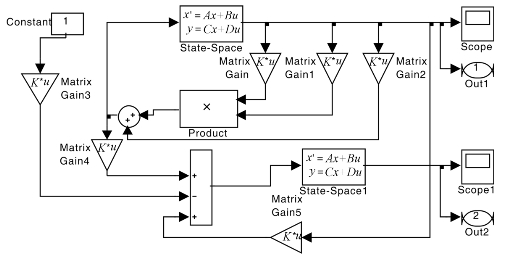
图5.1　Lorenz仿真系统模块

图5.1中State－Space是驱动系统状态模块，State－Space1是响应系统状态模块，Matrix Gain-Matrix Gain5是具有不同参数设置的矩阵增益模块，Constant是常数模块，out1和out2分别是驱动系统和响应系统的输出模块。矩阵增益模块通过各种运算构成驱动—响应系统的输入项，满足上述条件。

5.1.3.2　LC振子及其仿真系统设计

超混沌是指至少有两个正的Lyapunov指数来表征轨迹的发散特性，只存在于非线性高维系统中，即至少具有四维的非线性复杂系统。超混沌LC振子系统是由A.Tamasevicius等提出的，其动力模型可描述为

(www.xing528.com)

公式（5.1－15）中，a、b、c、d、μ和ε均为系统参数。l（u）为阶跃函数，满足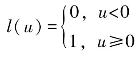。当系统参数a＝0.6，b＝0.05，c＝0.015，d＝10，ε＝0.33，μ＝0.3时，系统有两个正的Lyapunov指数，即λ1＝0.11，λ2＝0.06，系统处于超混沌状态。

同理，按照公式（5.1－12）将公式（5.1－15）分解成线性和非线性部分，并引入可调参数β，得到线性系数矩阵A及其对应的非线性函数Φ（x）

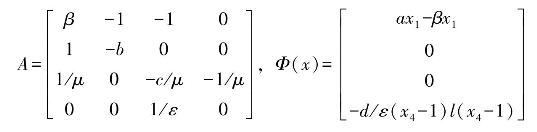
这里，选取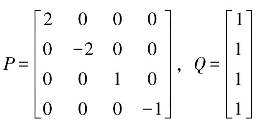。设β＝1，B＝［0　0　1　0］T，可以验证，rank（ctrb（A，B））＝4，即矩阵A和B可控。取极点J＝［－2　－1　－0.2＋0.1i　－0.2－0.1i］T，则增益矩阵K＝［－2.993 9　3.398 9　4.300 0　－3.298 6］。该系统广义同步误差e＝［e1　e2　e3　e4］T为四维向量。假设初始值x0＝［0.1　0.34　－1.024　2.034］T，y0＝［0.21　－0.43　1.024　1.034］T。按照以上值的设定，利用Matlab7.1中的Simulink模块构建仿真系统，图5.2是构造的超混沌LC振子仿真系统。

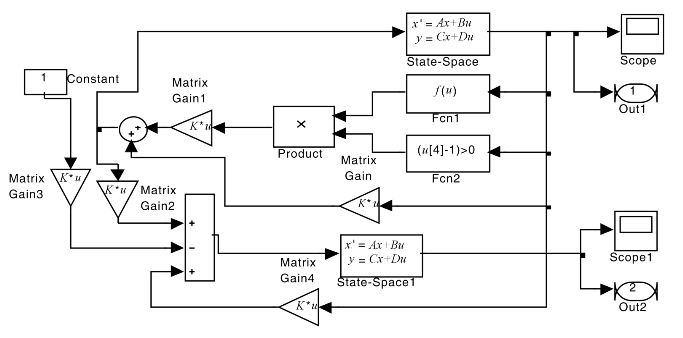
图5.2　LC振子仿真系统模块

图5.2中State－Space是驱动系统状态模块，State－Space1是响应系统状态模块，Matrix Gain～Matrix Gain4是分别具有不同参数设置的矩阵增益模块，Fcn1和Fcn2是函数模块，Constant是常数模块，out1和out2分别是驱动系统和响应系统的输出模块。矩阵增益模块和函数模块通过各种运算构成驱动—响应系统的输入项，满足上述条件。

5.1.3.3　仿真结果与误差分析

图5.3～图5.5为在CPU为PentiumⅣ2.60 GHz，内存大小为512 MB，硬盘大小为80 G的计算机上运行的仿真结果。图5.3为Lorenz混沌系统和LC振子系统驱动系统吸引子轨迹。

图5.3　驱动系统吸引子轨迹

（a）Lorenz驱动系统吸引子　（b）LC驱动系统吸引子

图5.4为Lorenz混沌系统和LC振子系统响应系统吸引子轨迹。

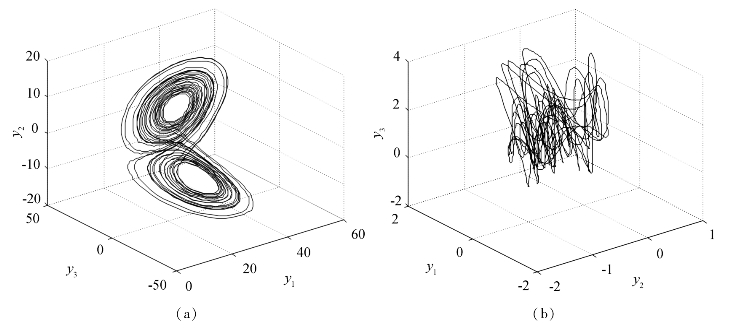
图5.4　响应系统吸引子轨迹

（a）Lorenz响应系统吸引子　（b）LC响应系统吸引子

图5.5为Lorenz混沌系统和LC振子系统广义同步系统误差曲线。

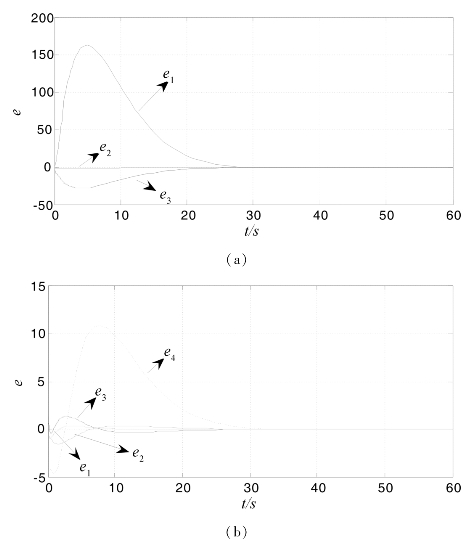
图5.5　广义同步系统误差曲线

（a）Lorenz系统误差曲线　（b）LC系统误差曲线

从图5.3和图5.4可知，两个系统的驱动与响应子系统的吸引子有明显差异。然而，从图5.5（a）可知，经过大约50 s后，Lorenz系统广义同步误差趋近于0，两子系统达到广义同步；从图5.5（b）可知，LC振子系统则经过大约30 s两子系统达到广义同步。由此可见，模型（5.1－13）所构造的广义同步方法不仅适用于低维的混沌系统，而且也适用于高维的超混沌系统。