现代控制理论及其应用研究

控制理论是一门高度综合的交叉学科，处于数学、计算机科学和工程技术科学相互作用的前沿，并且与自然科学和管理科学的各门分支也有密切的联系。控制理论所提供的一般性理论和方法在众多方面对技术进步和社会发展起着至关重要的作用。

5.1.1.1　系统状态空间模型

在现代控制理论中，一个控制系统可用数学模型来描述。常用的模型有传递函数模型、零极点增益模型和状态空间模型。各种模型各有其特点，有时为了计算和实现方便需要在各种模型之间进行转换。在混沌控制理论中，通常采用状态空间模型来描述动力系统。所谓状态空间是指以状态变量x1，x2，…，xn为基底所构成的n维空间。状态空间模型又可以分为连续状态空间模型和离散状态空间模型。

连续状态空间模型的数学描述为

其中，x为状态向量，y为输出向量，u为输入向量。A、B、C和D为系数矩阵。

离散状态空间模型的数学描述为

公式（5.1－2）表示k时刻状态向量x与输出向量y的表达式。A、B、C和D为系数矩阵，u为输入向量。

5.1.1.2　能控性与能观性

系统的能控性和能观性是控制理论中两个重要的概念，是设计控制器和状态估计器的基础。能控性是指系统状态在输入作用下转移到指定的状态的能力，而能观性是指从输出中反映系统状态的能力。

对于n维连续定常系统

如果存在一个分段连续的输入u（t），在有限时间区间内使系统由初始状态转移到指定的任一终端状态，则此状态是能控的。若系统的所有状态都是能控的，则此系统是状态完全能控的，即满足：

即称系统能控，否则系统不能控。其中，cam为能控矩阵。

同理，如果对任意给定的输入u，在有限观测时间内，通过输出能唯一地确定系统在初始时刻的状态，则此状态是能观测的。若系统的每个状态都是能观测的，则称此系统是状态完全能观测的。可构造能观性矩阵(www.xing528.com)

当其秩rank（cav）＝n，则称系统能观，否则系统不能观。对于离散系统，能控性与能观性亦有类似的结果。

5.1.1.3　极点配置

自然界中各物理量之间的变换关系可以用函数的形式表示，而这些函数同时满足微分方程。由特征方程的解决定微分方程解的形式，而特征方程的解就称为系统的极点。给定控制系统，通过选择反馈增益矩阵，使闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的动态性能，即为极点配置。极点配置是基于状态反馈的，即u＝Kx。因此，为了使系统达到期望的极点，关键在于求出增益矩阵K。

实现极点配置的步骤为：

（1）检查系统的可控性，当rank（cam）＝rank［A，AB，A2B，…An－1B］＝n时系统可控；

（2）确定系统矩阵A的特征多项式系数ai

（3）确定变换矩阵T

其中，w＝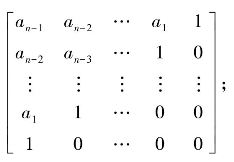

（4）确定期望特征多项式系数Ai

（5）求增益矩阵K

将求得的增益矩阵K代入控制系统反馈项，可得到期望极点u1，u2，…un，完成系统的极点配置。对于采用状态反馈的系统，进行任意配置极点的充要条件是系统状态完全可控。