混沌同步及其在图像加密中的应用研究-应用实例与分析

为了验证定理4.4给出的自适应同步控制方法的正确性和有效性，本节将给出一系列仿真实例。此外，还分析了分数阶q和反馈增益ki对同步效果的影响。

在本节的数值仿真中，采用分数阶Chen系统作为驱动网络的节点，分数阶Financial系统作为响应网络的节点，分数阶次均取为q＝0.96，网络的大小取为N＝5，驱动网络和响应网络的外部耦合配置矩阵分别为：

即驱动网络和响应网络具有不同的拓扑结构。为简便起见，内部耦合矩阵选取为A＝I3，网络中节点状态的初始值xij（0），yij（0）（i＝1，2，…，5，j＝1，2，3）在（－10，10）范围内任意选择，比例因子矩阵选为k＝diag（1，－2，3，2，－1）。驱动网络和响应网络的同步误差表示为eij（t）＝yij（t）－αixij（t）（i＝1，2，…，5；n＝1，2，3）。根据定理4.4，条件（4.4－5）只是实现修正投影外同步的充分条件，这里，选择耦合强度矩阵为K＝diag（20，15，5，16，10），相应的同步误差曲线如图4.15、图4.16和图4.17所示。

图4.15给出了两个复杂网络修正投影外同步误差ei1的曲线图。

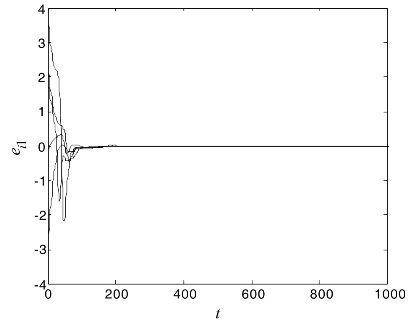
图4.15　修正投影外同步误差ei1曲线图

图4.16给出了两个复杂网络修正投影外同步误差ei2的曲线图。

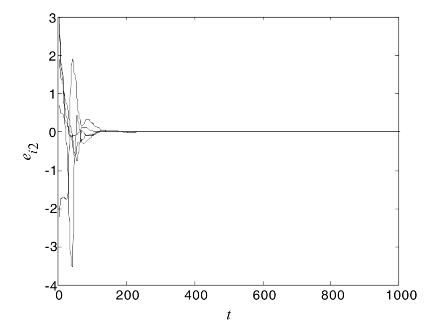
图4.16　修正投影外同步误差ei2曲线图

图4.17给出了两个复杂网络修正投影外同步误差ei3变化的曲线图。

图4.17　修正投影外同步误差ei3曲线图(www.xing528.com)

图4.15、图4.16和图4.17的实验结果表明，自适应控制方法可以实现两个不同结构的复杂网络之间达到修正投影外同步。

研究结果表明，分数阶的值q和耦合强度的值ki对同步效果有很大的影响。为了从总体上描述驱动网络和响应网络的同步过程，定义修正投影外同步的平均同步误差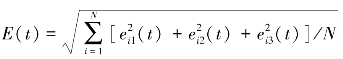，由该定义可以看出，当E（t）趋向于0时，我们可以实现修正投影外同步。

首先，考虑耦合强度不变，仅改变分数阶q的值。当q＝0.8，q＝0.9和q＝0.99时，同步误差E（t）随时间变化的曲线如图4.18所示。由此可以看出，随着分数阶q值的增大，同步效果变得越来越好。

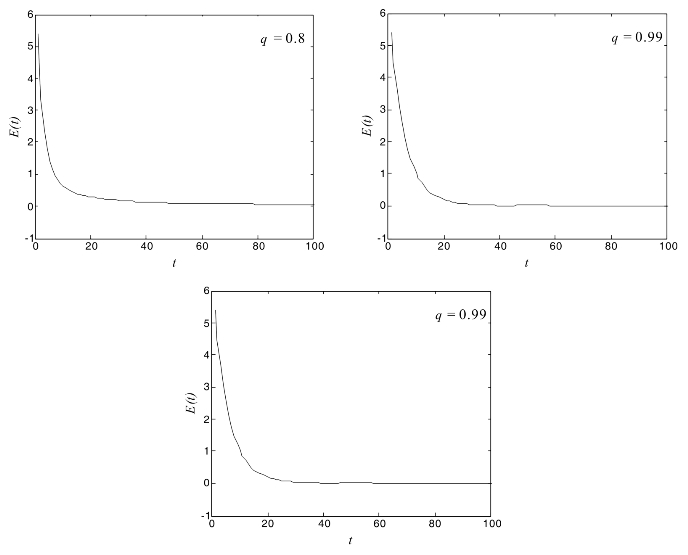
图4.18　分数阶q取不同值的同步误差E（t）变化曲线图

其次，不改变分数阶q的值，仅修改耦合强度K的值，为了简化问题，设k1＝k2＝k3＝k4＝k5。当q＝0.96，ki＝5和ki＝35（i＝1，2，…，5）时的同步误差E（t）随时间变化的曲线如图4.19所示。

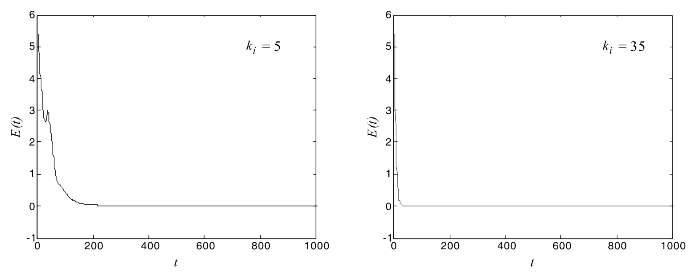
图4.19　耦合强度ki取不同值的同步误差E（t）变化曲线图

从图4.19我们可以看出，随着耦合强度值ki的增大，外同步的速度明显加快。不仅如此，即使某些耦合强度ki的值变为0时，修正投影外同步仍然可以实现，只是同步的速度会明显变慢。当分数阶仍为q＝0.96，耦合强度设为k1＝k2＝k3＝10，k4＝k5＝0和k1＝10，k2＝k3＝k4＝k5＝0时，平均同步误差E（t）随时间变化的曲线如图4.20所示。

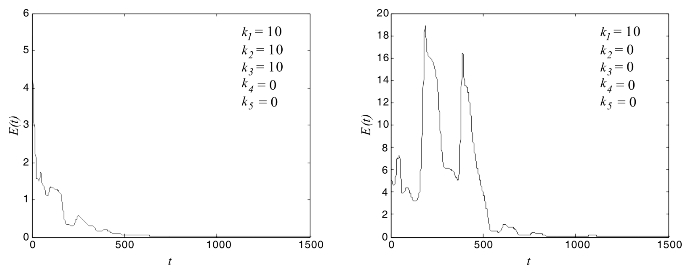
图4.20　某些耦合强度ki取0值的同步误差E（t）变化曲线图

以上实验结果表明，不同的分数阶次和不同的耦合强度会在很大程度上影响复杂网络外同步的速度。总体来说，分数阶次和耦合强度的值越大，外同步的速度会越快。同时，即使某些耦合强度的值为0，外同步仍然能够实现，只是外同步的速度会慢一些，这就需要我们在实际应用中在同步控制代价和同步速度二者之间做折中。