系统间修正函数投影同步误差变化情况|混沌同步与图像加密研究

为了验证提出的不同阶分数阶混沌系统的修正函数投影同步方法的有效性，本节给出两个仿真实例，分别对m＞n时的降阶同步和m＜n时的升阶同步进行数值仿真。具体地，降阶同步使用超混沌Lorenz系统驱动混沌Chen系统，升阶同步使用混沌Arneodo系统驱动超混沌Lü系统。本节统一采用预估—校正法对分数阶微分系统进行数值求解。

4.3.4.1　m＞n时降阶修正函数投影同步

当驱动系统的阶数大于响应系统的阶数时，采用降阶的方式来统一两个混沌系统的阶数。本节将分数阶超混沌Lorenz系统和分数阶Chen系统作为实例，使得超混沌Lorenz系统驱动参数未知的Chen系统按照某些时间函数的关系进行演化。

分数阶超混沌Lorenz系统的动态方程为

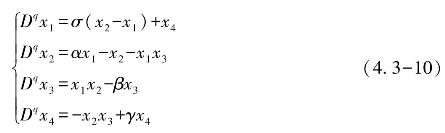
当系统参数选择为（α，β，γ，σ）＝（10，28，8／3－1），q1＝q2＝q3＝q4＝q＝0.998时，分数阶系统表现出超混沌特性，系统在x1－x2－x3平面和x2－x3－x4平面的投影如图4.9所示。

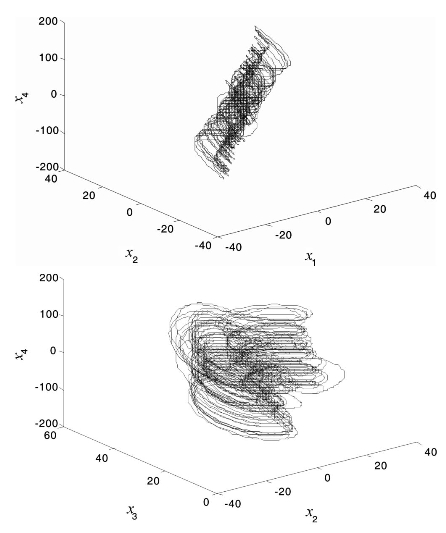
图4.9　分数阶超混沌Lorenz系统的混沌吸引子

1999年，陈关荣教授在研究混沌反控制的过程中发现了Chen系统，Chen系统与Lorenz系统非常类似，并且互为对偶系统，但Chen系统与Lorenz系统在拓扑结构上并不等价，它具有更复杂的拓扑结构和动力学行为。分数阶Chen系统可以写为

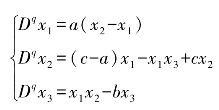
其中，分数阶次满足0＜q≤1，系统参数取值为q＝35，b＝3，c＝28。研究表明，Chen系统表现出混沌特性的最低总阶次为2.1，当q＝0.8时，分数阶Chen系统的混沌吸引子如图4.10所示。

为了实现超混沌Lorenz系统与Chen混沌系统之间的降阶修正函数投影同步，将系统（4.3－10）在x1－x2－x3平面的投影作为驱动系统，具体形式为

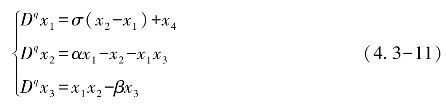
参数未知的受控的响应系统定义为

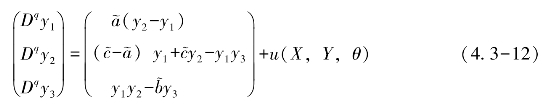
其中，为系统的未知参数。

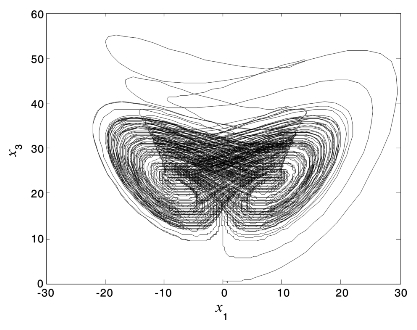
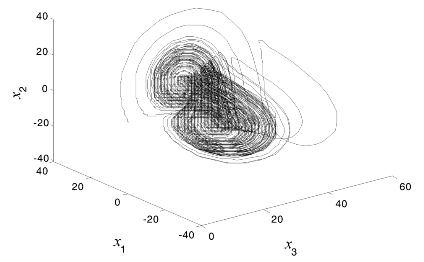
图4.10　分数阶Chen系统的混沌吸引子

根据4.3.3节中的讨论，可以得到b1（X，Y，θ）的值为

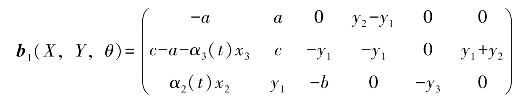
因此，未知参数的参数更新律和实矩阵b2（X，Y，θ）可以选择为

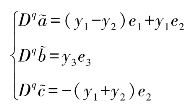
和

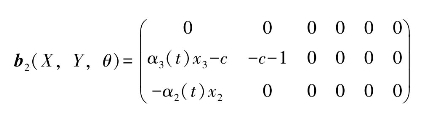
即控制器设计为

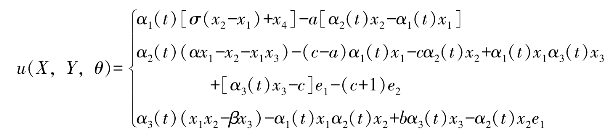
根据b1（X，Y，θ）、b2（X，Y，θ）和参数更新律的设计，容易得到如下矩阵

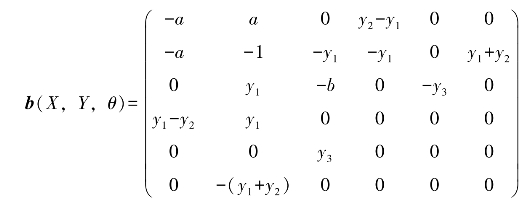
显然，矩阵b（X，Y，θ）中的元素满足定理4.3中的两个条件，即误差系统渐近稳定。这样，降阶系统（4.3－11）和系统（4.3－12）能够实现修正函数投影同步，同时，能够准确估计出响应系统的未知参数。

本节的数值仿真中，系统（4.3－10）的系统参数选择为（σ，α，β，γ）＝（10，28，8／3，－1），响应系统（4.3－12）的系统参数的真实值选为θ＝（a，b，c）＝（35，3，27）。选择比例函数矩阵为Λ（t）＝diag（1＋sin（t），2＋t，2－0.8cos（t）），系统（4.3－10）和响应系统（4.3－12）的初始值分别为（x1（0），x2（0），x3（0），x4（0））＝（2，－1，1，1）和（y1（0），y2（0），y3（0））＝（1，0，3），因此，误差系统的初始值为（e1（0），e2（0），e3（0））＝（－1，2，1.8），未知参数的初始值为（（0））＝（30，1，25），两个系统的分数阶次选择为q＝0.95。对应的数值仿真结果如图4.11和图4.12所示。

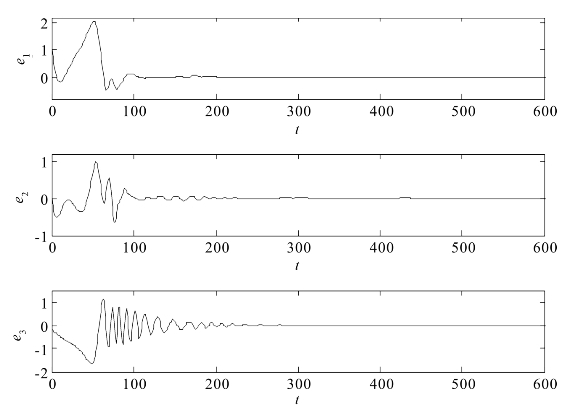
图4.11给出了驱动系统（4.3－11）和响应系统（4.3－12）之间的同步误差曲线图，可以看出，随着时间的推移，降阶之后的驱动系统（4.3－11）能够与响应系统（4.3－12）实现修正函数投影同步。

(www.xing528.com)

图4.11　系统（4.3－11）和系统（4.3－12）的修正函数投影同步误差曲线图

图4.12给出了响应系统（4.3－12）的3个未知参数的真实值的估计过程，从图4.12中可以看出，在进行参数估计时，随着时间的推移，响应系统（4.3－12）的未知参数的估计值逐渐趋向于相应的真实值a＝35，b＝3，c＝27。

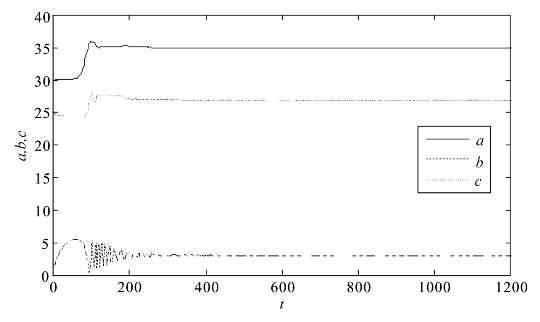
图4.12　Chen系统（4.3－12）的未知参数估计时间演化

本节提出的修正函数投影同步方法能够实现超混沌系统与混沌系统之间的同步，并且能够准确地识别响应系统的未知参数。

4.3.4.2　m＜n时升阶修正函数投影同步

当m＜n时，即驱动系统的阶数小于响应系统，本节采用分数阶Arneodo系统来驱动分数阶超混沌Lü系统。为了验证本节所提方法能够适用于响应系统参数已知的情况，这里设响应系统Lü系统的参数是已知的。为了使得驱动系统的阶数与响应系统相同，将驱动系统Arneodo系统的阶数提高1，将它变成一个四维混沌系统，并设计合适的控制器，使它与超混沌Lü系统达到同步。

分数阶超混沌Lü系统的具体形式为

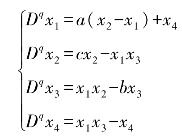
当系统参数为a＝36，b＝3，c＝20时，系统表现出超混沌特性，q＝0.95时的混沌吸引子如图4.13所示。

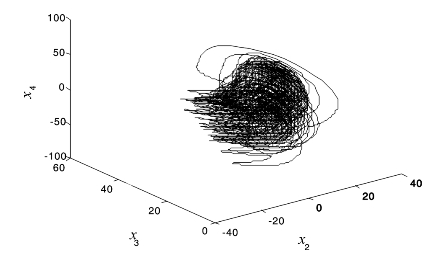
图4.13　q＝0.95时，分数阶超混沌Lü系统的混沌吸引子

分数阶Arneodo系统可以表示为

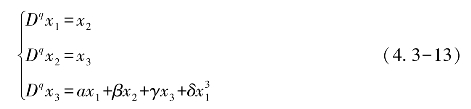
受控的分数阶超混沌Lü系统的方程为

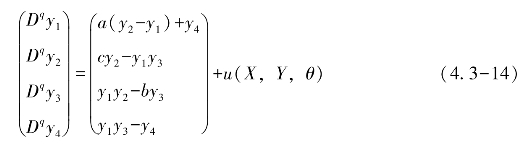
基于4.3.2节中讨论的升阶方案，为分数阶Arneodo系统（4.3－13）构建一个辅助状态变量x4，设该变量的分数阶导数为Dqx4＝x1（1－x2），此时，驱动系统可以表示为

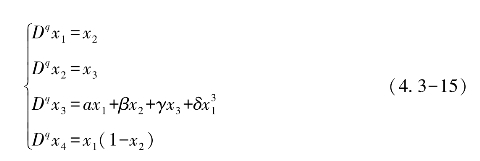
根据4.3.3节讨论的修正函数投影方法，可以得到矩阵

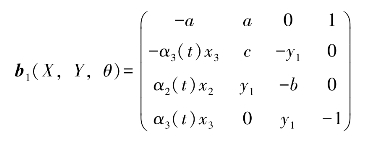
这样，我们可以选择b2（X，Y，θ）为

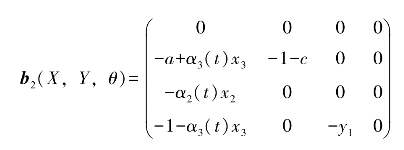
即控制器设计为

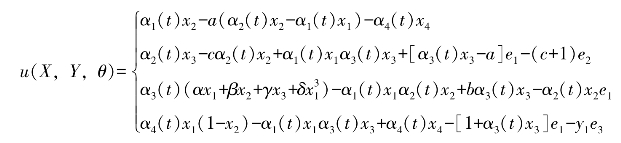
根据b1（X，Y，θ）和b2（X，Y，θ）的值，可以得到矩阵b（X，Y，θ）的值为

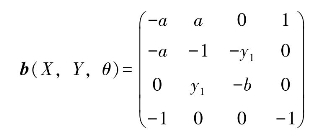
显然，矩阵b（X，Y，θ）中的元素满足定理4.3中的两个条件，则误差系统渐近稳定，这样，升阶后的驱动系统（4.3－15）和响应系统（4.3－14）能够实现修正函数投影同步。图4.14给出了系统（4.3－15）和系统（4.3－14）之间的修正函数投影同步误差的变化情况。

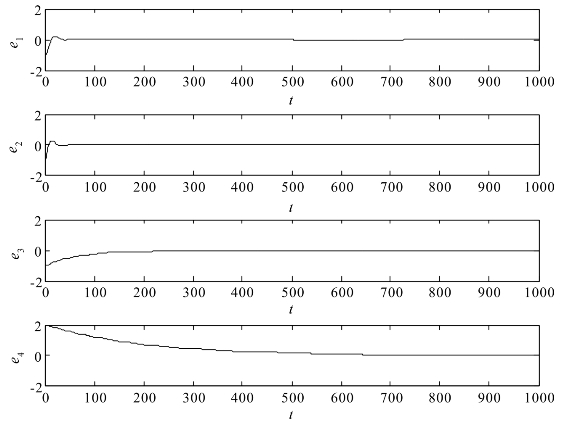
图4.14　系统（4.3－15）和系统（4.3－14）的修正函数投影同步误差

从图4.14的仿真结果可以看出，当响应系统的参数已知时，可以将低阶的三维混沌系统升阶为四维系统，并通过本节所提的修正函数投影方法实现升阶的驱动系统与响应系统按照一个比例函数矩阵同步演化。