OPCL耦合实现失配分数阶混沌系统的同步

针对定理4.1和定理4.2给出的修正投影同步判定标准，本节给出两个数值仿真实例，分别讨论参数失配情况下对称系统和非对称系统的OPCL耦合同步，对于没有参数失配的情况，只需将参数失配值设为0，这里不再给出具体实例。

4.2.2.1　参数失配情况下对称系统的耦合同步

本节将带有参数失配的对称分数阶Lorenz系统作为驱动系统，将分数阶Financial系统作为响应系统，基于OPCL耦合实现对称分数阶系统的修正投影同步。

著名气象学家E.N.Lorenz在简单的数学模型中发现了“混沌”现象，他将有限振幅自由对流模式近似得到流体力学方程，经过简化和边界条件处理得到了Lorenz系统的方程，其分数阶形式可以表示为

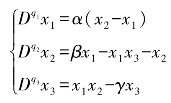
其中，分数阶次满足0＜q1，q2，q3≤1，系统参数取值为α＝10，β＝28，γ＝8／3。当系统具有非整数阶次时，即当系统所有阶次总和∑＝q1＋q2＋q3＜3时，系统仍然能够表现出混沌特性。但变量∑是有阈值的，研究表明，∑＝2.91是分数阶系统周期运动与混沌运动的界限，只有当∑＞2.91时，系统的运动轨迹是混沌的。当q1＝q2＝q3＝q＝0.998时的混沌吸引子如图4.1所示。

图4.1　q＝0.998时分数阶Lorenz系统的混沌吸引子

Financial动态模型描述了利率、投资需求以及价格指数这3个状态变量随时间的变化情况，分数阶Financial系统定义为

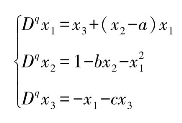
其中，x1表示利率，x2表示投资需求，x3表示价格指数，a表示储蓄金额，b表示投资成本，c表示市场的需求弹性。影响x1改变的主要因素包括两个方面：一是来自投资的矛盾，即投资和储蓄之间的差距；二是价格的结构调整。x2的变化率与投资率、投资成本和利率成反比。x3的变化一方面受供给和需求之间的矛盾控制，另一方面受膨胀率的影响。当系统参数为a＝3，b＝0.1，c＝1阶数q≥0.85时，该系统具有混沌特性。q＝0.95时的混沌吸引子如图4.2所示。

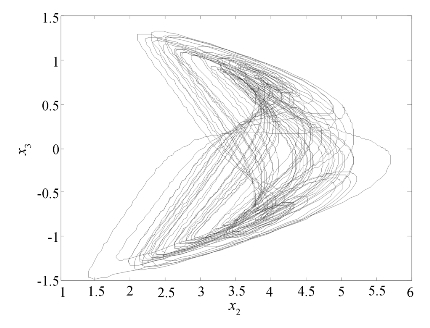
图4.2　q＝0.95时，分数阶Financial系统的混沌吸引子

带有参数失配的对称分数阶Lorenz系统可以表示为

其中，Δα、Δβ和Δγ分别为参数α、β和γ对应的失配值。

受控的分数阶Financial系统定义为

当系统参数为a＝3，b＝0.1，c＝1，阶数q≥0.85时，该系统具有混沌特性。

根据4.2.1节中基于OPCL耦合控制的修正投影同步方法，首先获得系统（4.2－7）的Jacobian矩阵

根据该Jacobian矩阵，响应系统的常数矩阵H选择为

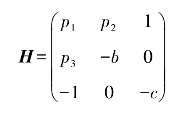
根据定义4.2，修正投影同步的误差向量可以表示为

由此可以得到受控的响应系统为

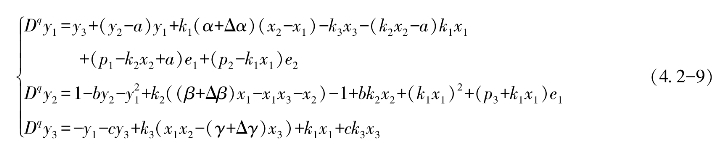
此时，只要我们选择合适的p1、p2、p3，误差向量（4.2－8）即可实现渐近稳定。根据定理4.1，我们选择p1＝－30，p2＝－10，p3＝10。在下面的数值仿真中，为了进一步降低耦合的复杂性，将驱动系统（4.2－6）的参数失配设置为Δα＝0.01，Δβ＝0和Δγ＝0。系统的分数阶次取q＝0.998，比例常数向量选择k＝（2，－1，－3），设驱动系统和响应系统的初始状态为（x1（0），x2（0），x3（0））＝（－1，－1，－1）和（y1（0），y2（0），y3（0））＝（0，1，2），则误差系统的初始状态为（e1（0），e2（0），e3（0））＝（2，0，－1）。采用预估—校正法来求解分数阶微分方程，相应的数值仿真结果如图4.3和图4.4所示。

图4.3给出了驱动系统（4.2－6）和响应系统（4.2－9）相应状态变量随时间的变化情况，可以看出，所有状态变量都按照比例常数矩阵中的比例因子进行同步演化。状态曲线x1的振幅一直保持为y1振幅的2倍，状态x2和状态y2按照等振幅向相反的方向运动，即实现反相同步，状态x3按照3倍于状态y3的振幅，向相反的方向运动。

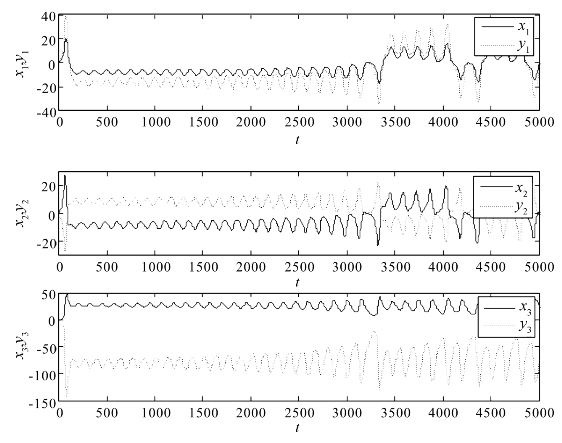
图4.3　系统（4.2－6）和系统（4.2－9）的状态时间演化

图4.4给出了两个分数阶系统的误差状态轨迹，随着时间的推移，3个误差状态变量均渐近趋向于0，表明驱动系统（4.2－6）和响应系统（4.2－9）达到修正投影同步。

图4.4　系统（4.2－6）和系统（4.2－9）的同步误差时间演化

这两组仿真实验结果表明，OPCL耦合可以实现带参数失配的不同分数阶混沌系统的修正投影同步。(www.xing528.com)

4.2.2.2　参数失配情况下非对称系统的耦合同步

本节将非对称分数阶Arneodo系统和非对称分数阶Lü系统作为实验对象，验证基于OPCL耦合方法的非对称分数阶系统修正投影同步的正确性。

通过对分数阶Arneodo系统的混沌行为进行研究，研究发现，系统所有阶次总和小于3时，分数阶Arneodo系统的混沌行为仍然存在，该系统表现出混沌特性的最低总阶次为2.1，分数阶Arneodo系统定义为

当系统参数为（α，β，γ）＝（5.5，－3.5，－1）时，Arneodo系统是混沌的。q＝0.95时的混沌吸引子如图4.5所示。

Lü系统将Lorenz系统与Chen系统连接在一起，完成了Lorenz系统向Chen系统的过渡，通过对分数阶Lü系统的混沌动态性进行研究，分数阶Lü系统是一个简单的三维自治系统

其中，系统的阶次满足0＜q≤1，参数使用a＝36，b＝3，c＝20。

图4.5　q＝0.95时，分数阶Arneodo系统的混沌吸引子

通过不断的仿真实验测试，要保证系统具有混沌特性，系统的分数阶次最低为q＝0.3，这是所有发现分数阶混沌系统的文献报道中的最低阶次的混沌系统。Lü系统的阶次q＝0.5时的混沌吸引子如图4.6所示。

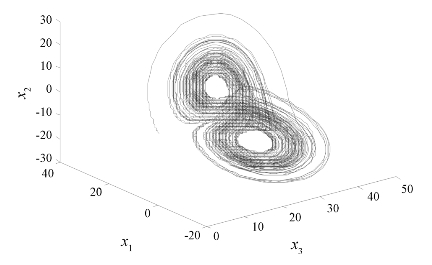
图4.6　q＝0.5时，分数阶Lü系统（4.8）的混沌吸引子

带有参数失配的非对称分数阶Arneodo系统可以表示为

其中，系统的阶次q1≠q2≠q3，Δα、Δβ和Δγ为系统参数α、β和γ对应的失配值。

设分数阶Arneodo系统（4.15）为驱动系统，受控的响应系统为分数阶Lü系统

基于4.2.1节中基于OPCL的修正投影同步方法，获得系统（4.2－11）的Jacobian矩阵

据此将响应系统的常数矩阵H选择为

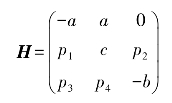
由此可以得到响应系统（4.2－11）中的控制器为

这里，只要我们选择合适的p1、p2、p3和p4，误差向量（4.2－8）即可实现渐近稳定。根据定理4.2，我们选择p1＝－30，p2＝0，p3＝0和p4＝0，其中p1决定了实现修正投影同步的速度。

现将非对称分数阶系统的阶次取为（q1，q2，q3）＝（0.9，0.92，0.96），根据定理4.2，最小公倍数m＝50，计算得到的Δ（λ）如下

通过解方程（4.2－12），我们可以得到min（｜arg（λi）｜）＝0.045 2＞π／2m＝0.031 4，因此，同步误差系统（4.2－8）渐近稳定，系统（4.2－10）和系统（4.2－11）达到修正投影同步。

数值仿真中，为了进一步降低OPCL耦合的复杂性，将驱动系统（4.2－10）的参数失配设置为Δα＝1、Δβ＝0和Δγ＝0。比例常数向量选择为k＝（1，－2，3），系统（4.2－10）和系统（4.2－11）的初始条件分别设置为（x1（0），x2（0），x3（0））＝（2，－1，1）和（y1（0），y2（0），y3（0））＝（1，－2，3）。采用预估—校正法来求解分数阶微分方程，相应的数值仿真结果如图4.7和图4.8所示。图4.7给出了驱动系统（4.2－10）和响应系统（4.2－11）相应状态变量随时间的变化情况，可以看出，所有状态变量都按照比例矩阵中的比例因子k＝（1，－2，3）进行同步演化。

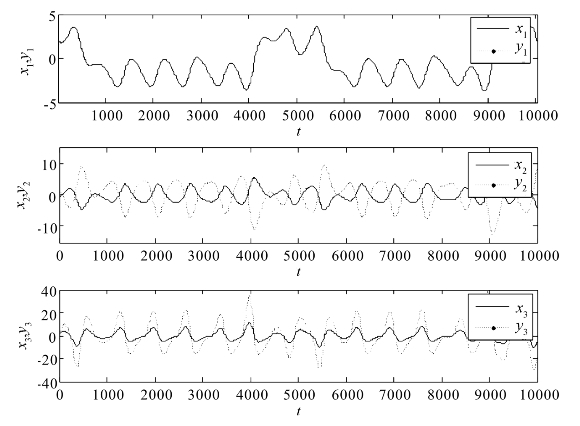
图4.7　系统（4.2－10）和系统（4.2－11）的状态时间演化

驱动系统的状态x1和响应系统的状态y1达到了完全同步，响应系统的状态y2以2倍于驱动系统的状态x2的振幅向相反的方向运动，响应系统的状态y3以3倍于驱动系统的状态x3的振幅向相同的方向运动。

图4.8　系统（4.2－10）和系统（4.2－11）的同步误差时间演化

图4.8给出了两个系统的修正投影同步误差状态轨迹，随着时间的推移，3个误差状态变量均渐近趋向于0，进一步验证了驱动系统（4.2－10）和响应系统（4.2－11）达到修正投影同步。以上两组仿真实验结果表明，基于OPCL耦合方法可以实现非对称分数阶系统的修正投影同步。