分数阶系统求解方法研究

由于分数微分的定义不允许在时域仿真中直接进行分数算子的运算，为了有效分析分数阶混沌系统的行为，人们常常采用整数阶拟合分数阶的方式，利用整数阶微分的求解方法来对分数阶微分进行运算，实际应用中用的比较多的是预估—校正法。

预估—校正法是在求解一阶微分方程组的Adams-Bashforth-Moulton方法的基础上推广得到的，其主要思想是通过运用分数阶微分的定义，对分数阶微分方程进行离散化的处理，最后运用迭代的方法对分数阶微分方程进行求解。这种方法是直接在时域内完成求解的，不仅能够将分数阶系统的求解误差控制在尽量小的范围内，而且不会损失分数阶系统固有的特性，为研究分数阶混沌系统及其应用提供了强大的数学支持。

考虑分数阶微分方程

初始值为y（k）（0）＝y（k）0，k＝0，1，…，m－1，m＝［α］，与其等价的Volterra积分方程为

令，tn＝nh，n＝0，1，2，…，N∈Z＋，对Volterra积分方程进行Adams-Bashforth预估，可得如下预估表达式

其中，bj，n＋1＝［（n－j＋1）α－（n－j）α］，然后再进行Adams-Moulton校正得到如下的校正表达式(www.xing528.com)

yh（tn＋1）＝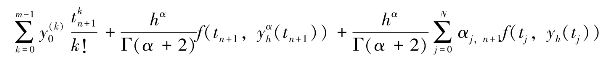

其中，

设α＞0且对某个T满足（t）∈C2［0，T］，该数值计算的最大误差为

采用预估—校正法求解分数阶混沌系统通常会花费较多的时间，但能够得到准确的结果，在实际工程中的应用范围较广。