混沌同步在图像加密中的硬件实现

为了验证3.2.1节和3.2.2节中介绍的同步方案的可用性，本节将应用Multisim仿真软件分别对这两种同步方案进行硬件实现。这种硬件实现的原理还是根据3.1.2.1节中介绍的连续混沌系统的硬件实现方法，其详细过程这里不再赘述。本节主要将给出同步方案中响应系统的电路图和同步的结果图。

3.2.3.1　线性反馈同步方案的硬件实现

本节以Lü超混沌系统为例，介绍运用线性反馈同步方案所构造出的响应系统的硬件实现以及所产生的同步结果。需要说明的是，驱动系统的电路与3.1.2.2节中的图3.9是一样的，这里由于篇幅原因不再赘述。此方案中参数值的选取与3.2.1.2节中一致。

图3.19为Lü超混沌系统线性反馈同步方案的响应系统的电路图。只要把图3.9中的变量y1和变量w1同时反馈到图3.19所标示的位置，就可以实现Lü超混沌系统的同步。

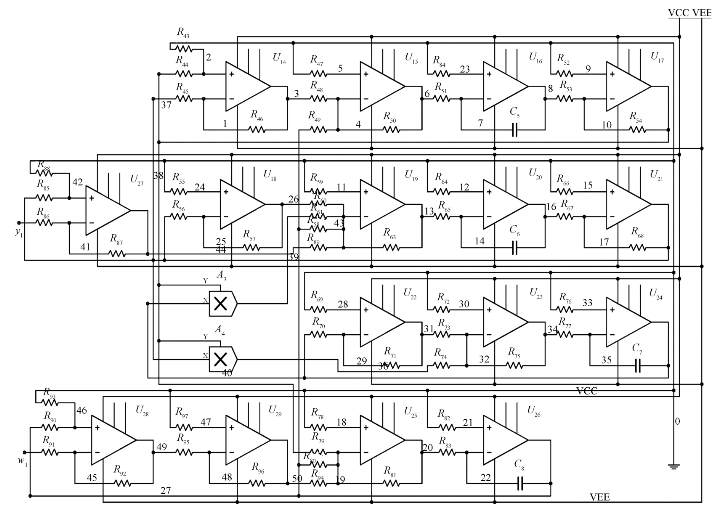
图3.19　线性反馈同步中的响应系统

图3.19中的电源电压为±15 V，放大器的放大倍数为30倍，其余各个元器件的值分别为：电阻R43和R46的阻值为30 kΩ；电阻R44、R45、R49、R51、R53、R54、R56、R58、R64、R65、R67、R68、R72、R76、R77、R82、R83、R84、R85、R86、R90、R91、R92和R93的阻值都为1 kΩ；R48、R50、R60、R61、R62和R63的电阻值为10 kΩ；R47的电阻值为833 Ω；电阻R52和R66的阻值为500 Ω；R55的电阻值为957 Ω；R57的电阻值为22.2 kΩ；R59的电阻值为714 Ω；R69和R70电阻值为15 kΩ；R71的电阻值为44 kΩ；R73、R74、R75、R81和R94的电阻值为3 kΩ；R79的电阻值为2 kΩ；R80的电阻值为6 kΩ。R87和R88的电阻值80 kΩ；电容C5、C6、C7、C8的电容值为10 μF。图3.20给出了由图3.19给出的电路图所产生的响应系统的运行轨迹随驱动系统的运行轨迹变化的情况。需要说明的是，由于在硬件实现中，驱动系统和响应系统之间达到同步所需的时间很短，甚至可以忽略不计，因此，图3.20中分别运用驱动变量和响应变量作为坐标轴的x轴和y轴。

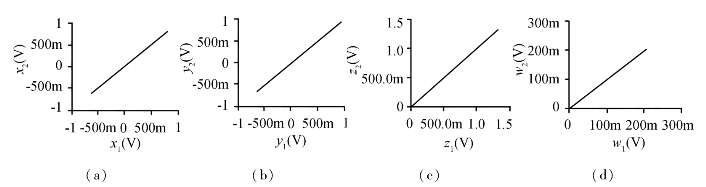
图3.20　当α＝0.8时，驱动系统和响应系统的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

从图3.20中可以看出，状态变量的值均处于对角线上，说明了驱动系统和响应系统达到了同步，从而证明了这种线性反馈同步方案的物理可实现性，为以后对该超混沌系统应用的研究奠定了良好的基础。

图3.21给出了α＝0时超混沌系统的线性反馈同步的状态变量同步图。

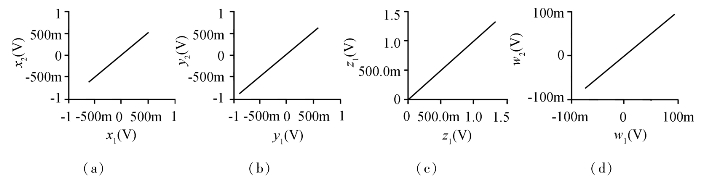
图3.21　当α＝0时，驱动系统和响应系统的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

图3.22给出了α＝0.95时超混沌系统的线性反馈同步的状态变量同步图。

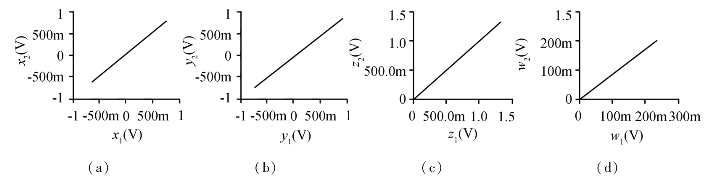
图3.22　当α＝0.95时，驱动系统和响应系统的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

鉴于篇幅原因及各参数表示系统之间具有极大的相似性，这里不再给出α＝0和α＝0.95这两种情况下响应系统的电路图。从图3.21和图3.22中可以看出这两种情况都取得了良好的同步效果。(www.xing528.com)

3.2.3.2　驱动—响应同步方案的硬件实现

本节同样以Lü超混沌系统为例，给出运用驱动—响应同步方案所构造出的响应系统的硬件实现以及所产生的同步结果。此方案中的驱动系统同样可以参考3.1.2.2节中的图3.9。

图3.23为Lü超混沌系统的驱动—响应同步方案中的响应系统的电路图。只要把图3.9中的x1、y1和w1同时反馈到图3.22所标示的位置，即可实现Lü超混沌系统的驱动—响应同步。

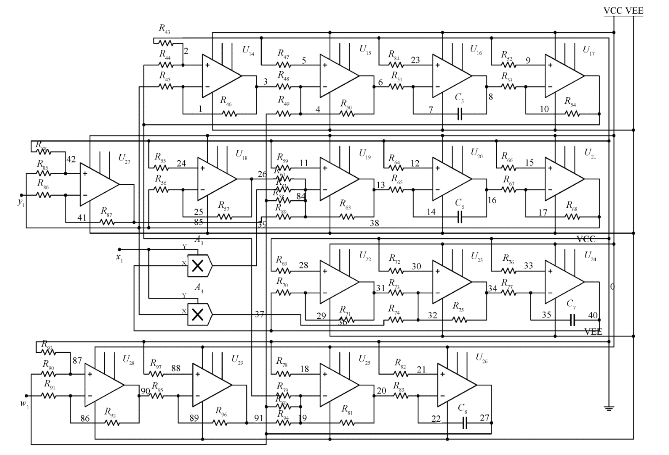
图3.23　驱动—响应同步中的响应系统

图3.23中电源电压为±15 V，放大器的放大倍数为30，其余各个元器件的值分别为：电阻R43和R46的阻值为30 kΩ；R44、R45、R49、R51、R53、R54、R56、R58、R64、R65、R67、R68、R72、R76、R77、R82、R83、R84、R85、R86、R90和R91的电阻值都为1 kΩ；R48、R50、R60、R61、R62和R63的电阻值为10 kΩ；电阻R47的阻值为833 Ω；R52和R66的电阻值为500 Ω；R55的电阻值为957 Ω；R57的电阻值为22.2 kΩ；R59的电阻值为714 Ω；R69和R70的电阻值为15 kΩ；R71的电阻值为44 kΩ；R73、R74、R75、R81和R94的电阻值都为3 kΩ；R79、R92和R93的电阻值为2 kΩ；电阻R80的电阻值为6 kΩ；R87和R88的电阻值为33 kΩ；电容C5、C6、C7和C8的电容值为10 μF。图3.24给出了运用此电路图所产生的驱动系统和响应系统之间的状态变量的同步结果。

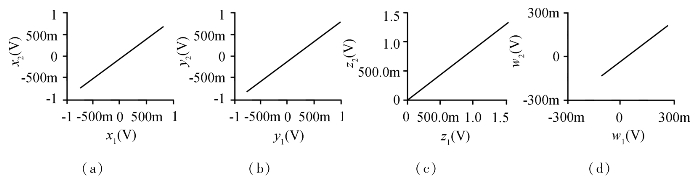
图3.24　驱动—响应同步的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

从图3.24中可以看出，驱动系统的状态变量和响应系统的状态变量之间的关系为偏向于横轴为45°角的直线，因此，可以认为它们达到了比较好的同步效果。同时还可以说明这种同步方案可以物理实现，为对超混沌系统应用的深入研究奠定了理论基础。

图3.25给出了α＝0时超混沌系统的驱动—响应同步的状态变量同步图。

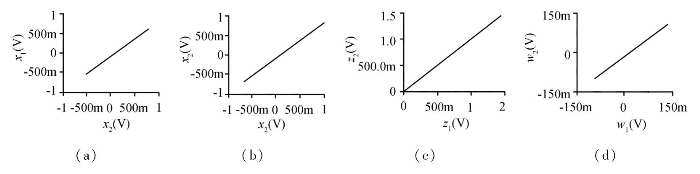
图3.25　当α＝0时，驱动—响应同步的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

图3.26给出了α＝0.95时超混沌系统的驱动—响应同步方案的状态变量同步图。

图3.26　当α＝0.95时，驱动—响应同步的状态变量同步图

（a）x1－x2　（b）y1－y2　（c）z1－z2　（d）w1－w2

鉴于篇幅原因及各参数表示系统之间的相似性，α＝0和α＝0.95这两种情况下响应系统的电路图就不再给出。从图3.25和图3.26同样可以看出，它们都取得了良好的同步效果，再一次证明了3.2.2节中所设计的驱动—响应同步方案的有效性。