线性反馈同步化设计的应用研究成果

3.2.1.1　线性反馈控制器的设计

为了运用线性反馈的同步方案实现3.1节构建的超混沌系统的同步，我们将公式（3.1－1）给出的超混沌系统作为驱动系统，同时将线性反馈控制器ui（i＝1，2，3，4）添加到驱动系统上作为响应系统，可以表示为

令驱动系统和响应系统之间的误差变量分别为e1＝x1－x2，e2＝y1－y2，e3＝z1－z2，e4＝w1－w2。则由驱动系统减去响应系统，得到误差系统的动力学方程为

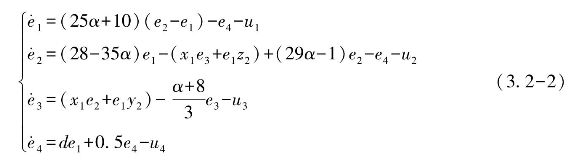
要使驱动系统和响应系统达到同步，误差系统需要满足‖e‖＝0，因此需要选择合适的线性反馈控制器。

需要说明的是，通过对混沌系统的基本特征进行分析，混沌系统是有界的，则新构建的超混沌系统一定存在4个正常量s1、s2、s3和s4，使得｜x（t）｜≤s1＜∞，｜y（t）｜≤s2＜∞，｜z（t）｜≤s3＜∞，｜w（t）｜≤s4＜∞成立。

定理3.1　当系统的线性反馈控制器设计为u1＝0，u2＝k1e2，u3＝0，u4＝k2e4，并且反馈控制系数k1和k2同时满足

（1）

（2）

其中，，A＝25α＋10＋f［（28－35α）＋s3］，B＝（25α＋10）（α＋8），驱动系统（3.1－1）和响应系统（3.2－1）能够达到完全同步。

证明：根据Lyapunov稳定性理论，要使驱动系统和响应系统达到同步，误差系统的动力学方程（3.2－2）在原点应是渐进稳定的，故可以选取Lyapunov函数为

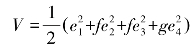
其中，E＝［｜e1｜　｜e2｜　｜e3｜　｜e4｜］T，A＝25α＋10＋f［（28－35α）＋s3］，

(www.xing528.com)

显然，为了使得误差系统的动力学方程（3.2－2）渐进稳定，矩阵P应该是正定的。因此，可以计算出，当且仅当反馈控制系数k1和k2同时满足不等式（1）和（2）时，矩阵P正定。证毕。

3.2.1.2　线性反馈同步化的仿真实验

为了验证所设计的同步控制器的有效性，对其进行了数值仿真。将驱动系统的初始状态设为：x1＝2，y1＝2，z1＝2，w1＝2；响应系统的初始状态为x1＝1，y1＝1，z1＝1，w1＝1。

当参数α＝0时，驱动系统的变量满足：｜x｜≤30、｜y｜≤28、5≤z≤50、｜w｜≤150，则常量s1、s2、s3和s4可以分别取为30、28、50和150。在此种情况下，当参数d＝10时，系统（3.1－1）呈现超混沌状态。根据定理3.1可以得到，反馈控制系数k1和k2的取值范围分别为k1＞209.774 2和k2＞1.422 7，因此选取k1和k2的值分别为210和2。图3.13给出了当参数α＝0、d＝10时，驱动系统和响应系统之间各个误差变量的演化过程。

图3.13　驱动系统和响应系统的同步误差曲线

从图3.13中误差变量随时间的变化情况可以看出，该控制器可以使得驱动系统和响应系统的输出很快地保持一致，从而说明了这种同步方案是有效的。图3.14和图3.15分别给出了当系统参数为d＝0.8和d＝0.95时，驱动系统和响应系统之间的误差变量随时间t的变化情况。

当参数α＝0.8时，驱动系统的变量满足：｜x｜≤30、｜y｜≤30、5≤z≤50、｜w｜≤150，则常量s1、s2、s3和s4可以分别取为30、30、50和150。根据3.1节中对系统（3.1－1）的动力学特性分析，当参数d＝15时，系统（3.1－1）呈现超混沌状态。根据定理3.1可以得到，反馈控制系数k1和k2的取值范围分别为k1＞181.457 7和k2＞1.023 9，故可以选取k1和k2的值分别为182和2。图3.14给出了驱动系统和响应系统之间各个误差变量的演化过程。

图3.14　驱动系统和响应系统的同步误差曲线

同理，当参数α＝0.95时，驱动系统的变量满足：｜x｜≤30、｜y｜≤30、5≤z≤50、｜w｜≤150，则常量s1、s2、s3和s4可以分别取为30、30、50和150。同样通过对系统（3.1－1）动力学特性进行分析得到，当参数d＝20时，系统处于超混沌状态。根据定理3.1可以得出，反馈控制系数k1和k2需要满足k1＞190.612 1和k2＞1.460 1才能使得驱动系统和响应系统的步调相一致，因此选取k1和k2的值分别为191和2。图3.15给出了此种情况下，驱动系统和响应系统之间各个误差变量的演化过程。

图3.15　驱动系统和响应系统的同步误差曲线

同样从图3.14和图3.15可以看出，驱动系统和响应系统在很短的时间内都能达到同步。纵观图3.13～图3.15可以发现，第4维的误差变量虽然在刚开始一小段时间内会呈现非同步化趋势，但很快就会向着同步演化，对整体的同步效果也没有影响。不过这种同步方案中，驱动系统中变量的最大值s1、s2、s3和s4的选取是通过一定的估计得到的。为了确保在选取不同的初始值时都能够使得吸引子在所选取的区间内，故其值的选取可能会比实际值要大一些，这样反馈控制系数k1和k2的取值范围就会比实际的范围要小一些。