超混沌系统的物理实现及其应用研究

随着对混沌在数学、通信等科学和工程领域的深入研究，许多构造混沌与超混沌吸引子的方法也随之而产生。但大多数的国内学者对混沌的研究仅仅停留在理论分析和数值仿真上，很少对混沌电路进行完整而深入的研究。而在实际的电路中存在很多的随机因素是很难进行模拟的，使得混沌系统所具有的复杂性和随机性等优势得不到充分的利用，其结果的可信度也不高。对混沌系统硬件实现研究的落后必将限制混沌理论向实用化方向发展，所以对混沌系统硬件实现的研究是混沌学研究中必不可少的一个环节。

3.1.2.1　连续混沌系统的物理实现

运算放大器作为连续混沌系统物理实现的主要单元，是具有很高放大倍数的主要单元。在实际电路中，通常结合反馈网络共同组成某种功能模块。图3.4给出了运算放大器的符号与传输特性。图3.4（a）为集成运算放大器的符号，除图中给出的同相输入端、反相输入端和输出端外，还有未标出的正电源端和负电源端（单电源运放则为接地）。

图3.4　运算放大器符号与传输特性

图3.4（b）给出了集成运算放大器在开环应用时的电压传输特性。中间一段过零斜线为线性区，上下两段水平横线为饱和区（正、负饱和电压由运放所加正负电源大小决定）。当运放工作在线性区时，uo＝Auo×（uP－uN）。由于开环电压放大倍数Auo很高，输入很小的信号也足以使输出电压饱和，另外干扰信号也会使输出难以稳定。因此，要使运算放大器稳定工作在线性区，通常需引入深度负反馈。为便于分析，一般把运算放大器理想化，即认为其开环电压放大倍数和差模输入电阻无穷大。

理想运算放大器工作在线性区时，依据两条原则进行分析：

（1）由于开环电压的放大倍数无穷大，故正、负输入端的电位相等，简称为“虚短”特性；

（2）由于输入电阻无穷大，故两个输入端的输入电流为0，简称为“虚断”特性。

在连续混沌系统的硬件实现中常用到的运算放大器有：反相比例运算电路、同相比例运算电路、差分比例运算电路、积分运算电路和求和电路。图3.5给出了这些运算放大器的设计电路。

图3.5　常用的运算放大器

（a）反相比例运算电路　（b）同相比例运算电路　（c）差分比例运算电路
（d）积分运算电路　（e）反相求和运算电路　（f）正相求和运算电路

图3.5中各个运算放大器的工作原理：

（1）反相比例运算电路

如图3.5（a）所示，电阻R1引入反相输入信号uI，电阻RF引入深度负反馈，使运放工作于线性区。根据“虚短”和“虚断”的特点，很容易可以推出u＋＝u－＝0，i＋＝i－＝0，则同相和反相输入端皆为“虚地”，iI＝iF，即。由此可以得出

反相比例运算电路实际上是一个深度的电压并联负反馈的电路，因此电路中的输入电阻应该不大，而输出电阻要求很小。若式（3.1－6）中的RF＝R1，则Auf＝－1，称为单位增益倒相器。

（2）同相比例运算电路

如图3.5（b）所示，输入电压uI接至同相输入端，但是为保证引入的是负反馈，输出电压uo通过反馈电阻RF仍接到反相输入端，同时反相输入端通过电阻R1接地。为了使集成运放反相输入端和同相输入端对地的电阻一致，R2的阻值仍为R2＝R1∥RF。根据“虚短”和“虚断”的特点，很容易得出u＋＝u－＝uI，i＋＝i－，故

同相比例运算电路实际上是一个深度的电压串联负反馈的电路，因此电路中的输入电阻应该很大，而输出电阻要求很小。若式（3.1－7）中的RF＝0或者R1＝∞，则Auf＝1，称为电压跟随器。

（3）差分比例运算电路

如图3.5（c）所示，输入电压uI和u′I分别加在集成运放的反相输入端和同相输入端，从输出端通过反馈电阻RF接回到反相输入端。为了保证两个输入端对地的电阻平衡，同时为了避免降低共模抑制比，通常要求R1＝R2，RF＝R′F。在理想条件下，根据“虚断”原理和叠加原理可以得出反相输入端的电位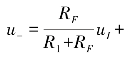为，而同相输入端的电位为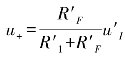。根据“虚短”原理可以得到

（4）积分运算电路

积分电路是应用比较广泛的模拟信号运算电路。它是组成模拟计算机的基本单元，用以实现对微分方程的模拟。同时，积分电路也是控制和测量系统中常用的重要单元，利用其充放电过程可以实现延时、定时以及各种波形的产生。将反相比例运算电路中的电阻RF用电容C代替作为负反馈元件，就成为积分运算电路，如图3.5（d）所示。同样根据“虚短”和“虚断”可以得出

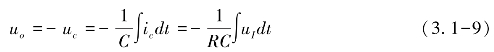
其中，RC为积分时间常数。

（5）反相比例求和电路

反相输入求和电路其实就是在反相比例运算电路的基础上加以扩展而得到的，如图3.5（e）所示。为了保证集成运放两个输入端对地的电阻平衡，同相输入端电阻R′的阻值应为R′＝R1∥R2∥R3∥RF。其输出电压值为

（6）同相比例求和电路

同相输入求和电路是在同相比例运算电路基础上扩展而成的，如图3.5（f）所示，其输出电压值为

在连续混沌系统的硬件实现中，常用的运算放大器是LM741运算放大器。一般的LM741运算放大器的最大工作电压为18 V。

对连续混沌系统进行硬件实现时，首先需要将系统的微分方程转化为积分方程。这是因为基本微分电路自身存在有一定缺陷，当输入信号频率升高时，电容的容抗减小，故放大倍数就会增大，造成电路对输入信号中的高频噪声非常敏感，因而输出信号中的噪声成分严重增加，使得信噪比大大下降；微分电路中的RC元件形成一个滞后的移相环节，它和集成运放中原有的滞后环节共同作用，很容易产生自激振荡，使电路的稳定性变差；输入电压发生突变时有可能超过集成运放允许的共模电压，以致使运放“堵塞”，使电路不能正常工作。除此之外，还可以从数学的角度来分析出微分方程自身的缺陷。标准的微分方程为

(www.xing528.com)

从公式（3.1－12）可以看出，函数x在t0时刻的微分值与它在t0＋Δt时刻的微分值有关，而我们知道混沌的下一时刻的值具有不可预测性，因此混沌系统的微分方程是不可以对其进行硬件实现的，我们需要将其转化为积分方程。

实验结果表明，如果直接按照微积分转化后的系统方程来搭建电路的话，运算放大器一般工作在饱和区，而不是线性区，使得在实际电路中根本看不到混沌波形。考虑到这些情况，还需要进行坐标变换，将电路信号缩小到能够使运算放大器工作在线性区的程度，以便能够看到清晰的混沌波形。通过扩大乘法器的倍数可以达到所期望的效果，一般在电路中使用的乘法器是AD633。

还有一个问题就是信号的频率。如果我们一味地按照前面所描述的方法去搭建电路的话，会发现混沌波形的实现速度十分缓慢，并且这样的混沌信号很难在模拟示波器上清楚地显示。在一般的模拟示波器上我们看到的只是按照混沌轨迹运动的一个亮点，这样对于研究混沌特性是毫无帮助的。为了在普通的模拟示波器上清楚地看到混沌和超混沌波形，必须提高信号的频率。而我们知道只有在积分运算电路中通过改变信号的频率，也就是可以通过减小电容值来提高混沌信号的频率。

3.1.2.2　超混沌系统的物理实现

超混沌系统中线性控制器＝dx＋ew硬件实现的电路图如图3.6所示，其中d＝R4／R2，e＝R4／R3。通过对系统（3.1－1）的研究知道，当α的取值分别为0、0.8和0.95时，d的取值范围分别为［3，24］、［11，50］和［15.3，45］，e的值为0.5。因此，d／e的最大值分别为48、100和90，也即R3／R2的最大值分别为48、100和90，从而说明R3和R2的阻值是有很大差异的。由于R3的阻值太大，导致R3中的电流很小。与R2中的电流相比，可能会小到忽略不计，从而达不到我们所构建的线性控制器的目的。

图3.6　线性控制器的电路图

为解决这一问题，需要将w的值减小10倍，故将系统（3.1－1）的动力学方程转化为

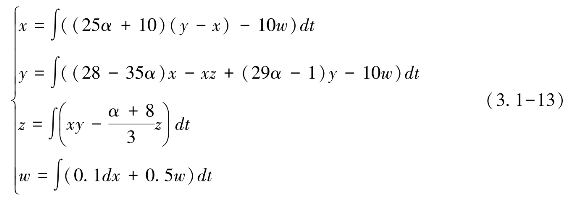
其中，α的值可以是0、0.8和0.95，d为待定常数。

根据3.1.2.1节中所描述的混沌系统电路的设计方法，设计了系统（3.1－1）的电路图，分别如图3.7、图3.8和图3.9所示，其中α的值分别是0、0.8和0.95。当α＝0时，超混沌系统的电路图如图3.7所示。

图3.7　当α＝0时，超混沌系统的电路图

图3.7中的电源电压为±15 V，放大器的放大倍数为30倍，其余各个元器件的值分别为：R1、R4、R6、R8、R18、R19、R20和R21的阻值为10 kΩ；R2、R3、R7、R9、R11、R12、R14、R16、R22、R23、R25、R26、R30、R34、R35、R40、R41和R42的阻值都为1 kΩ；R27、R28、R31、R32和R33的阻值为3 kΩ；R10和R24的阻值为500 Ω；R15的阻值为28 kΩ；R17的阻值714 Ω；R29的阻值8 kΩ；R5的阻值833 Ω；R13的阻值967 Ω；电容C1、C2、C3、C4的电容值都为10 μF。由于d的值是变化的，则图3.7中的R36、R37、R38、R39的电阻值也会随之变化，因此在这里没有给出它们的电阻值。但是，后面给出由其产生的相位图时，它们的电阻值将会全部给出。

通过模拟示波器观察由电路图3.7所产生的吸引子的x－z、z－w相位图，如图3.8所示。图3.8分别给出了超混沌吸引子和周期吸引子的相位图，其中参数d的值分别为5和24。当d＝5时，将R36、R37、R38和R39的电阻值分别设置为250 Ω、1 kΩ、1 kΩ和500 Ω。当d＝24时，R36、R37、R38和R39的电阻值分别为615 Ω、1 kΩ、4.8 kΩ和2.4 kΩ。

图3.8　图3.7所实现的相位图

（a）d＝5 x－z相位图　（b）d＝5 z－w相位图
（c）d＝24 x－z相位图　（d）d＝24 z－w相位图

图3.9给出了α值为0.8时超混沌系统（3.1－1）的电路图。

图3.9　当α＝0.8时，超混沌系统的电路图

图3.9中的电源电压值同样为±15 V。不过，其放大器的放大倍数需要调到40倍才能观察到清晰的吸引子。图中其他各个元器件的值分别为：R1和R4的阻值为30 kΩ；R2、R3、R7、R9、R11、R12、R14、R20、R22、R23、R25、R26、R30、R34、R35、R40、R41和R42的阻值都为1 kΩ；R6、R8、R18、R19和R21的阻值为10 kΩ；R5的阻值为833 Ω；R10和R24的阻值为500 Ω；R13的阻值为957 Ω；R15的阻值为22.2 kΩ；R17的阻值为769 Ω；R27和R28的阻值为15 kΩ；R29的阻值为4 kΩ；R31、R32和R33的阻值为3 kΩ；C1、C2、C3、C4的电容值为10 μF。

图3.10中给出了由电路图3.9所仿真实现的超混沌、周期和准周期吸引子，其中d的值分别为15、45和50。当d＝15时，R36、R37、R38和R39的电阻值分别为500 Ω、1 kΩ、3 kΩ和1.5 kΩ；当d＝45时，电阻R36、R37、R38和R39的值分别为750 Ω、1 kΩ、9 kΩ和4.5 kΩ；当d＝50时，R36＝769 Ω，R37＝1 kΩ，R38＝10 kΩ，R39＝5 kΩ。

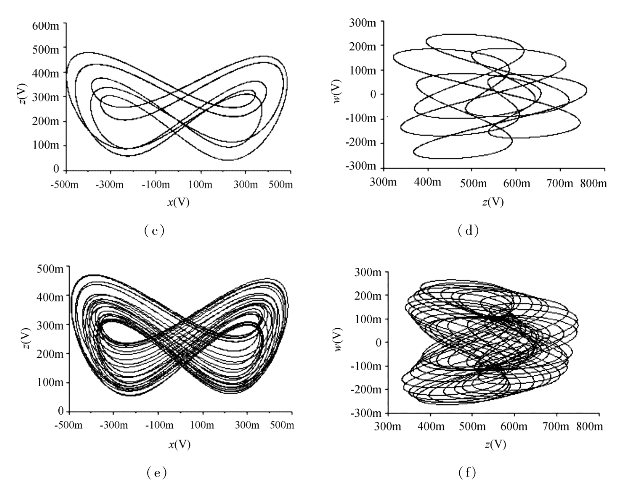
图3.10　由图3.9所产生的相位图

（a）d＝15 x－z相位图　（b）d＝15 z－w相位图　（c）d＝45 x－z相位图
（d）d＝45 z－w相位图　（e）d＝50 x－z相位图　（f）d＝50 z－w相位图

图3.11给出了α值为0.95时系统（3.1－1）的电路图。

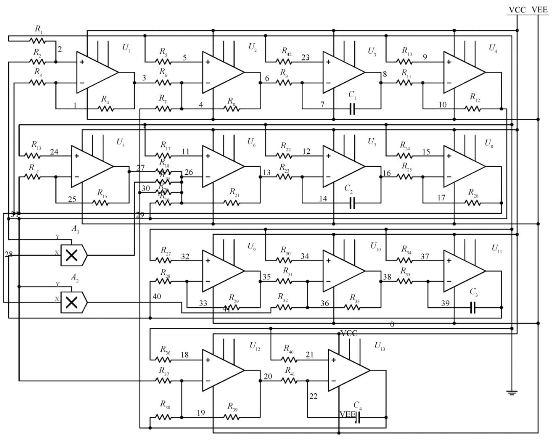
图3.11　α＝0.95时，超混沌系统的电路图

同图3.7一样，图3.11的电源电压值为15 V，放大器的放大倍数也为30倍。图3.11中其他元器件的值分别为：电阻R1和R4的阻值为33.75 kΩ；电阻R2、R3、R7、R9、R11、R12、R14、R22、R23、R25、R26、R30、R34、R35、R40、R41和R42的阻值都为1 kΩ；电阻R6和R8的阻值为10 kΩ；电阻R10和R24的阻值为500 Ω；电阻R15的阻值为26.55 kΩ；电阻R16的阻值为2 kΩ；电阻R17的阻值为575 Ω；电阻R18、R19和R21的阻值为10.5 kΩ；电阻R20的阻值为1.05 kΩ；电阻R27、R28、R31、R32和R33的阻值为3 kΩ；电阻R29的阻值为8.95 kΩ；电阻R5的阻值为833 Ω；电阻R13的阻值为966 Ω；电容C1、C2、C3和C4的电容值都为10 μF。跟图3.7所描述的相同，图3.11中的R36、R37、R38和R39的电阻值也在给出相位图时列出。

通过模拟示波器观察由电路图3.11所仿真实现的x－z和z－w相位图，如图3.12所示。图3.12呈现了3种典型的吸引子：超混沌吸引子、准周期吸引子和周期吸引子，此时参数d的值分别为20、38和40。当参数d＝20时，R36、R37、R38和R39的电阻值分别为571 Ω、1 kΩ、4 kΩ和2 kΩ，此时系统呈现超混沌状态；当参数d＝38时，R36、R37、R38和R39的电阻值分别为717 Ω、1 kΩ、7.6 kΩ和3.8 kΩ，此时系统呈现为准周期状态；当参数d＝40时，R36、R37、R38和R39的电阻值分别为727 Ω、1 kΩ、8 kΩ和4 kΩ，此时系统为周期态。

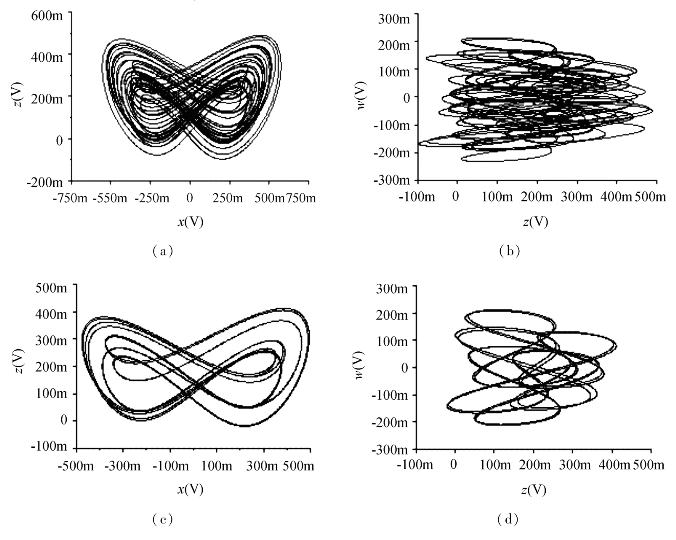
图3.12　由图3.11所产生的相位图

（a）d＝20 x－z相位图　（b）d＝20 z－w相位图　（c）d＝38 x－z相位图
（d）d＝38 z－w相位图　（e）d＝40 x－z相位图　（f）d＝40 z－w相位图

鉴于篇幅原因，其他平面的相位图这里不再列出。从清晰的超混沌吸引子、周期吸引子和准周期吸引子的轨迹可以说明超混沌系统的物理可实现性，为对其进一步深入的研究奠定了良好的基础。此外，我们发现用硬件实现所产生的相位图与用Matlab软件仿真实现的相位图是基本吻合的。