超混沌系统的动力学特性研究

3.1.1.1　对称性和不变性

显然，通过系统（3.1－1）的动力学方程可以看出：无论α，d取什么值，系统（3.1－1）在变换（x，y，z，w）→（－x，－y，z，－w）下都具有不变性，即系统（3.1－1）关于z轴具有对称性，并且对于所有的系统参数这种对称性都成立。除此之外，z轴本身也是系统的一条解轨线，即若t＝0时有x＝y＝0，则对于所有的t＞0都有x＝y＝0。进一步讲，当t→∞时，z轴上所有的解轨线均趋近于原点。

3.1.1.2　耗散性和吸引子的存在性

对于系统（3.1－1），很容易得出

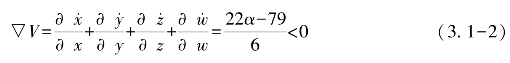
由于0≤α≤1，系统（3.1－1）始终是耗散的，并且以公式（3.1－3）给出的指数形式收敛。

也就是说，一个初始体积为V（0）的体积元在时间t时收缩为体积元V（0）e（22α－79）t／6。这也意味着，当t→∞时，包含系统轨线的每个体积元都会以指数速率收缩到0。因此，所有的系统轨线会被限制在一个特定的区域上。从而说明了吸引子的存在性，但对于吸引子的形状尚不能确定，有待于进一步研究。

3.1.1.3　平衡点及其稳定性

平衡点的稳定与否决定着系统的运动轨迹是否稳定。只有当动力系统的平衡点不稳定时，系统才有产生混沌或者超混沌的可能性，因此平衡点的稳定性在许多实际问题中具有至关重要的作用。

系统（3.1－1）的平衡点可以根据计算方程组

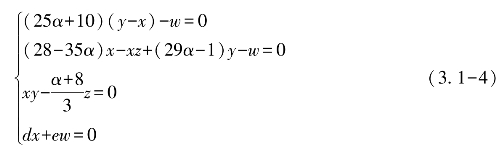
得到，具体结果为：

（1）当0＜d＜12.5α＋5时，系统（3.1－1）有如下三个平衡点：

E0＝（0，0，0，0）　E1＝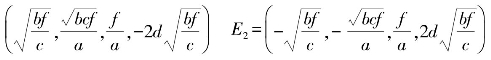

其中，变量a、b、c和f分别表示为a＝25α＋10，b＝（α＋8）／3，c＝25α＋10－2d，f＝（27－6α）（25α＋10）＋2d（11－4α）。

（2）当d≥12.5α＋10时，系统（3.1－1）只存在唯一一个平衡点E0。

为了降低计算的复杂性，只对E0点的稳定性进行分析研究。在E0点线性化系统（3.1－1），得到相应的Jacobian矩阵为

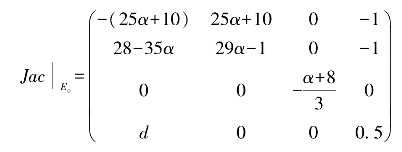
通过计算该系统的特征方程，得到一个特征值和一个关于λ的三次特征多项式f（λ）＝λ3＋β·λ2＋γ·λ＋ε，其中ε＝－〔75α2＋（4d－307.5）α－（135＋11d）〕，β＝10.5－4α，γ＝150α2－613α－275.5＋d。根据Routh-Hurwitz准则，当且仅当满足不等式组

时，平衡点E0为稳定的。而在α分别取0、0.8和0.95时，d的取值范围分别为［3，24］、［11，50］、［15.3，45］。通过计算得到方程组（3.1－5）无解，也即E0点为不稳定的平衡点，从而说明了系统（3.1－1）具有产生超混沌现象的可能性。

3.1.1.4　Lyapunov指数谱

对于一个四维自治系统，其Lyapunov指数与系统轨道之间具有如下对应关系：

（1）对于超混沌轨道，系统的Lyapunov指数有2个为正，1个为0，1个为负；

（2）对于混沌轨道，系统的Lyapunov指数有1个为正，1个为0，2个为负；(www.xing528.com)

（3）对于周期轨道，系统的Lyapunov指数有1个为0，3个为负；

（4）对于准周期轨道，系统的Lyapunov指数有2个为0，2个为负。

为了研究系统（3.1－1）的动力学特性，对于不同α值时的系统进行数值仿真实验，得到其Lyapunov指数。根据公式（3.1－1）的描述，将α的值分别设定为0、0.8和0.95，同时参数d的变化范围分别是［3，24］、［11，50］和［15.3，45］，其实验结果分别如图3.1～图3.3所示。需要注明的是，将系统的Lyapunov指数值分别记为λ1、λ2、λ3和λ4。

当α＝0时，系统（3.1－1）随着d变化时的Lyapunov指数谱如图3.1所示。

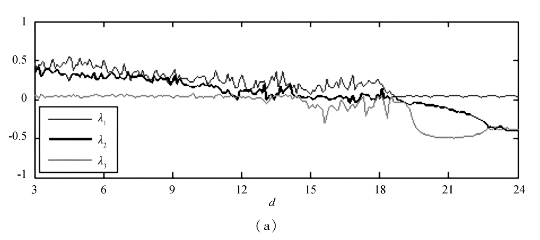
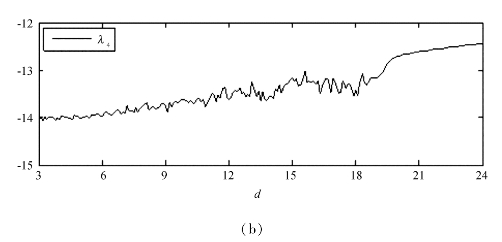
图3.1　当α＝0时，系统（3.1－1）随着d变化时的Lyapunov指数谱

图3.1中横坐标的起始值为3。从图3.1中不难发现，随着参数d的变化，Lyapunov指数谱很明显的能被分为3段。当d取［3，14.9］时，系统（3.1－1）有2个正的Lyapunov指数，1个零的Lyapunov指数和1个负的Lyapunov指数，并且2个正的Lyapunov指数都很明显的大于0，说明系统（3.1－1）处于超混沌状态。相对于整个区域而言，系统的超混沌区域的跨度是比较大的。当d取［15，18.8］时，系统（3.1－1）有1个正的Lyapunov指数，1个0的Lyapunov指数和2个负的Lyapunov指数，说明系统（3.1－1）处于混沌状态。另外，在区间［18.9，24］内，系统（3.1－1）有1个0的Lyapunov指数和3个负的Lyapunov指数，系统（3.1－1）处于周期状态。从而说明了，当参数α＝0时，随着参数d的变化，系统呈现出不同的动力学行为，即超混沌状态、混沌状态和周期状态。

当α＝0.8时，系统（3.1－1）随着参数d变化时的Lyapunov指数谱如图3.2所示。

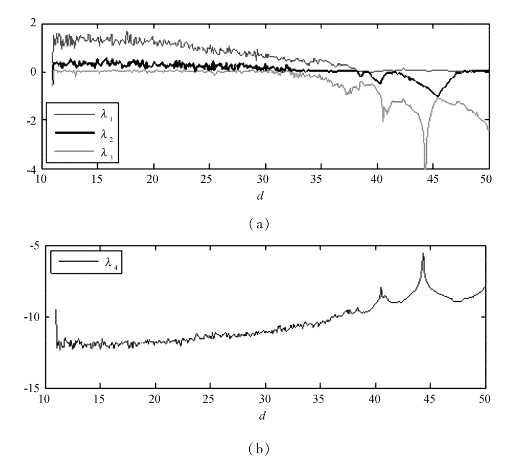
图3.2　当α＝0.8时，系统（3.1－1）随着d变化时的Lyapunov指数谱

图3.2中横坐标的起始值为11。从图3.2中同样可以发现，随着参数d的变化，Lyapunov指数谱也能明显地被分成几个部分。不过，与图3.1不同的是，图3.2可以被分成5部分，从而也说明了当α＝0.8时系统可能具有更为复杂的行为。从图3.2中可以看出：

（1）当d取［11.1，31.2］时，系统（3.1－1）有2个正的Lyapunov指数，1个0的Lyapunov指数和1个负的Lyapunov指数，说明系统（3.1－1）处于超混沌状态；

（2）当d取［32.6，38.3］时，系统（3.1－1）有1个正的Lyapunov指数，1个0的Lyapunov指数和2个负的Lyapunov指数，说明系统（3.1－1）处于混沌状态；

（3）当d在区间［38.4，47.6］时，系统（3.1－1）有1个0的Lyapunov指数和3个负的Lyapunov指数，系统（3.1－1）处于周期状态；

（4）这个系统还存在一个新颖之处就是它的准周期轨道，在区间［47.7，50］之内，系统（3.1－1）有2个0的Lyapunov指数和2个负的Lyapunov指数，此时系统（3.1－1）处于准周期状态。

另外，区间［31.3，32.5］是一段既有混沌现象又有超混沌现象的震荡区域。从而说明了，当α＝0.8时，随着参数d的变化，系统（3.1－1）不仅呈现出超混沌、混沌、周期的动力学行为，而且还呈现出了稳定的准周期区域，并且其超混沌区域也是相当宽阔的。与α＝0时的系统相比，α＝0.8时系统的动力学特性更为复杂。

当α＝0.95时，系统（3.1－1）随着参数d变化时的Lyapunov指数谱如图3.3所示。

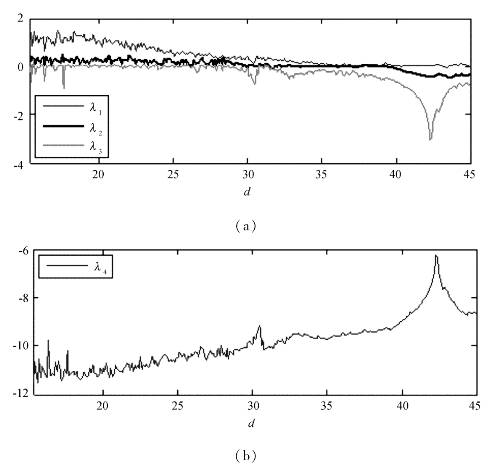
图3.3　当α＝0.95时，系统（3.1－1）随着d变化时的Lyapunov指数谱

图3.3中横坐标的起始值为15.3。从图3.3中可以看出，随着参数d的变化，Lyapunov指数谱也很明显地被分为4段。当d取［15.3，29.6］时，除去点16.3、17、17.1、17.6之外，系统（3.1－1）有2个正的Lyapunov指数，1个0的Lyapunov指数和1个负的Lyapunov指数，并且2个正的Lyapunov指数都很明显的大于0，说明系统处于超混沌状态。当d取［29.7，35.7］时，系统（3.1－1）有1个正的Lyapunov指数，1个0的Lyapunov指数和2个负的Lyapunov指数，系统处于混沌状态。当d取［35.8，39.7］时，系统（3.1－1）有2个零的Lyapunov指数和2个负的Lyapunov指数，此时系统处于准周期状态。当d取［39.8，45］时，系统（3.1－1）有1个0的Lyapunov指数和3个负的Lyapunov指数，此时系统处于周期状态。从而说明了，随着参数d的变化，系统呈现出不同的动力学行为，即超混沌、混沌、周期、准周期，并且该系统具有稳定的超混沌区域、混沌区域和宽阔的周期窗口。

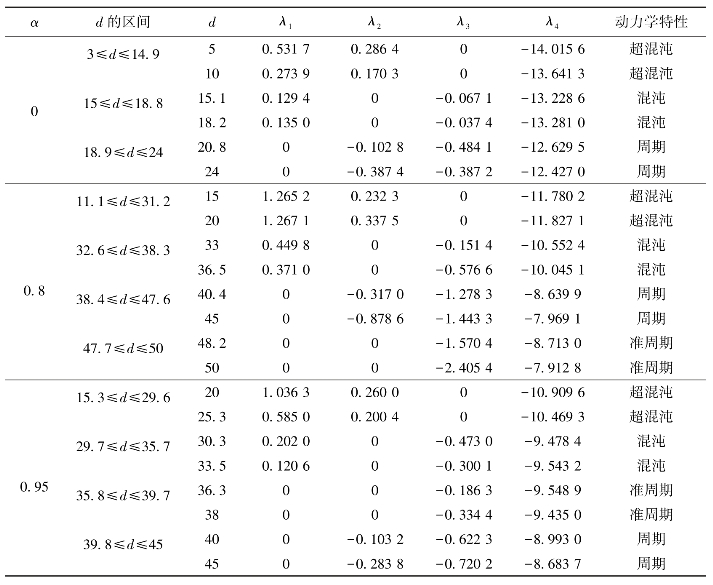
表3.1中给出了当α取值分别为0、0.8、0.95，d取一些典型值时，系统的Lyapunov指数值。从表3.1中可以看出，Lyapunov指数值的计算结果与Lyapunov指数谱中基本一致。

表3.1　系统（3.1－1）的典型Lyapunov指数值