实验结果分析：混沌同步在图像加密中的应用

定理2.3的证明过程表明，条件（A）（B）只是实现混合同步的充分条件。实验结果表明，当统一混沌系统参数α＝0.8时，控制增益只需满足k2＞4即可实现定义2.3给出的混合同步，但控制增益k2的大小能够控制混合同步的速度，k2的值越大，混合同步的速度越快，即误差变量收敛到原点所需的时间越少。

本节给出统一混沌系统参数取α＝0.8，响应系统参数已知情况的一组实验结果，如图2.12和图2.13所示。图2.12给出了k2＝5时的同步误差曲线。

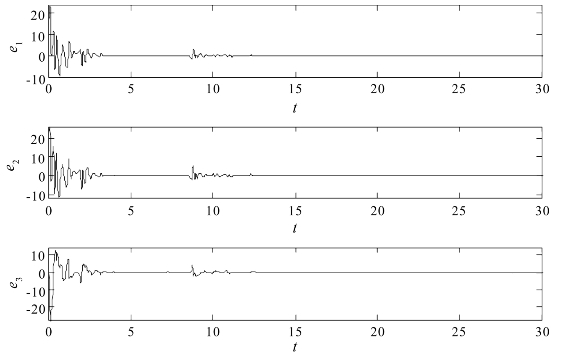
图2.12　k2＝5时耦合系统（2.1－8）和（2.3－1）的状态误差变化图

图2.13给出了k2＝14时的同步误差曲线。(www.xing528.com)

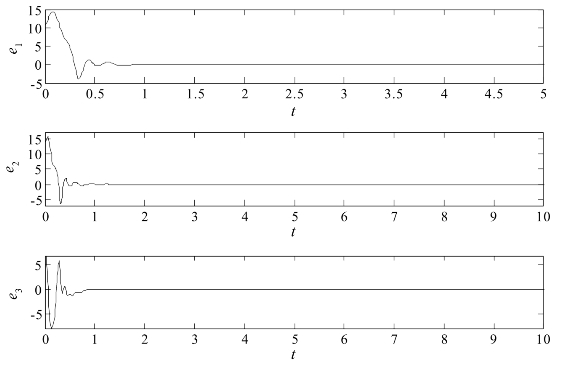
图2.13　k2＝14时耦合系统（2.1－8）和（2.3－1）的状态误差变化图

从图2.12和图2.13可以看出，与控制增益k2＝5时实现的混合同步相比，控制增益k2＝14时实现的混合同步所经历的过程要简单很多，同步速度会快一些。

本节的实验结果表明，对于具有对称性的统一混沌系统，仅在响应系统的第二维上附加一个简单的单项线性控制器即可实现混合同步。该混合同步方法具有良好的同步性能，能够实现同步误差的全局渐进稳定性，具有动态过程误差小、鲁棒性好和同步速度快的优点，即使在响应系统参数未知的情况下，也能保证混沌同步的精度足够高，而且能够准确识别未知参数的值。此外，与单个混沌系统相比，实现混合同步后的系统具有更高的复杂性和随机性，更适合应用在安全性要求较高的图像加密算法中。