仿真实验结果展示混沌同步及其在图像加密中的应用

为了验证仅在第二维附加线性控制器的混合同步控制方法的有效性和正确性，本节将给出一些数值仿真结果。由于参数已知情况和参数未知情况的同步控制条件一致，本节仅给出参数未知时的仿真结果。本节使用Matlab软件进行数值仿真，采用四阶龙格－库塔法求解耦合的统一混沌系统。本节的仿真结果中，驱动系统的初始状态取为（x1（0），y1（0），z1（0））＝（0.1，0.5，12），响应系统的初始状态取为（x2（0），y2（0），z2（0））＝（10.1，12.5，2）。响应系统未知参数的初始状态α1（0）＝0.5。

2.3.3.1　当α＝0时的仿真结果

当统一混沌系统的参数取α＝0时，根据定理2.4中的条件（A）（B），当k2＞94.05时（p＝16.3，M＝27和N＝1.3），系统（2.1－8）和（2.3－4）能够实现混合同步。当线性控制器的控制增益k2取95，未知参数按公式（2.3－6）更新时，系统（2.1－8）和（2.3－4）的混合同步结果如图2.5－图2.8所示。图2.5给出了驱动系统（2.1－8）和响应系统（2.3－4）对应状态变量x的变化趋势，容易看出，随着时间的变化，对应状态x呈现绝对值相同符号相反的反相同步。

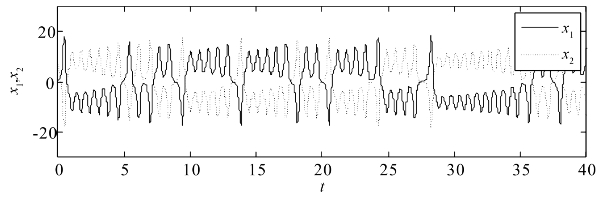
图2.5　α＝0时耦合系统（2.1－8）和（2.3－4）状态x的变化图

图2.6给出了驱动系统（2.1－8）和响应系统（2.3－4）对应状态变量y的变化趋势，容易看出，随着时间的变化，对应状态y呈现绝对值相同符号相反的反相同步。

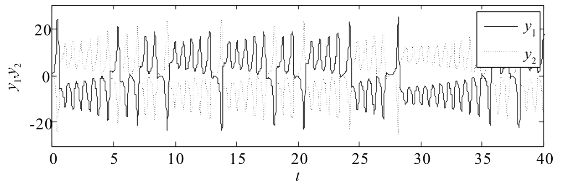
图2.6　α＝0时耦合系统（2.1－8）和（2.3－4）状态y的变化图

图2.7给出了驱动系统（2.1－8）和响应系统（2.3－4）对应状态变量z的变化趋势，容易看出，随着时间的变化，对应状态z则呈现幅值完全相同的正相同步。

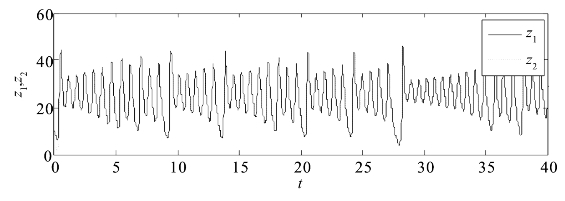
图2.7　α＝0时耦合系统（2.1－8）和（2.3－4）状态z的变化图

图2.8进一步给出了混合同步误差e1、e2和e3随时间t的变化曲线，可以看出，3个同步误差变量能够迅速收敛到原点。

图2.8　α＝0时耦合系统（2.1－8）和（2.3－4）的状态误差变化图(www.xing528.com)

图2.9给出了响应系统中未知参数α1的变化情况，由此可见，在公式（2.3－6）给出的参数更新律的控制下，随着时间的变化，响应系统（2.3－4）中的未知参数α1逐渐趋向于真实值0。

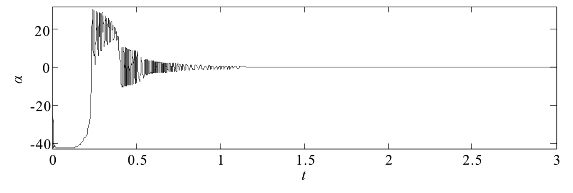
图2.9　α＝0时响应系统（2.3－4）的未知参数α1的变化图

从以上仿真结果可以看出，单项线性控制器u2＝－k2e2可以实现状态x和y呈现反相同步，而状态z为正相同步，即正相同步和反相同步共存的混合同步，同时，参数更新律（2.3－6）能够正确和有效地估计响应系统的未知参数。

2.3.3.2　当α＝0.8时的仿真结果

当统一混沌系统的参数取α＝0.8时，根据定理2.4，当k2＞113.8时，系统（2.1－8）和（2.3－4）能够实现混合同步，此时，各变量的取值为p＝6.3，M＝34和N＝1.5。当控制增益k2取114，未知参数按公式（2.3－6）进行更新时，系统（2.1－8）和（2.3－4）的混合同步结果如图2.10和图2.11所示。

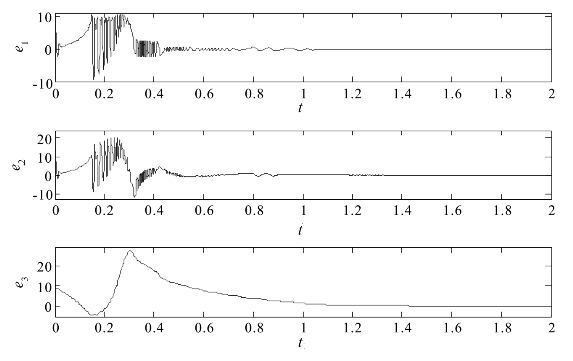
图2.10　α＝0.8时耦合系统（2.1－8）和（2.3－4）的状态误差变化图

图2.10表示耦合系统（2.1－8）和（2.3－4）的状态误差变化情况，图2.11表示响应系统（2.3－4）的未知参数的变化情况，由此可见，当α＝0.8时，正相同步和反相同步共存的混合同步同样能够实现，同时，响应系统的未知参数完全能够正确和有效地估计。

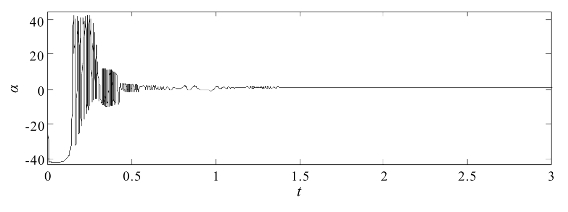
图2.11　α＝0.8时响应系统（2.3－4）的未知参数α1的变化图

以上两组仿真实验充分证明了本节所设计的单项线性控制器和参数更新律的有效性，能够实现参数未知情况下，耦合统一混沌系统中正相同步和反相同步共存。