系统参数已知的混合同步-混沌同步及其图像加密应用

对于系统（2.1－8）给出的驱动系统，当响应系统的参数已知时，只在第二维加控制的响应系统表示为

其中，控制器u2＝－k2e2。基于公式（2.1－10）定义的误差向量，系统（2.1－8）和（2.3－1）之间的误差动态系统为

系统（2.1－8）和（2.1－1）之间的混合同步等价于误差系统（2.3－2）在e＝0时的渐近稳定性。根据基于Lyapunov函数的稳定性理论，如果对于定常微分动力系统方程＝f（x）（x∈Rn）存在一个正定的Lyapunov函数V（x），其全导数（x）是负定的，即对于邻域D中所有点都有（x）＜0，则该方程的定点是渐近稳定的。

定理2.3　假设统一混沌系统具有有界性。对于驱动系统（2.1－8）和响应系统（2.1－1），设M为状态｜y1｜的最大值，N为状态z1的最小值，其中，y1和z1为系统（2.1－8）的两个状态变量，如果存在常数p＞0，使得条件

（A）4pbσ－M2＞0

（B）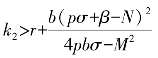

成立，则耦合系统（2.1－8）和（2.3－1）能够实现混合同步。其中，各参数的值为σ＝25α＋10，r＝29α－1，β＝28－35α和b＝（8＋α）／3。

证明：选择如下Lyapunov函数

其中，p＞0为常数。该函数是正定的，其导数可以表示为(www.xing528.com)

其中，

显然，为了保证误差系统（2.3－2）渐近稳定，矩阵Q必须是正定的。矩阵Q正定当且仅当下面3个条件满足：

（C）pσ＞0

（D）pσ（k2－r）－（pσ＋β－z1）2／4＞0

（E）pσb（k2－r）－（pσ＋β－z1）2b／4－（k2－r）／4＞0

容易看出，如果定理2.3中的条件（A）（B）满足，条件（C）～（E）就能满足。因此，根据Lyapunov稳定性理论，误差系统（2.3－2）在x＝0处渐近稳定，证毕。

定理2.3给出的条件（A）（B）表明，只要控制增益k2的值足够大，只在响应系统的第二维上设置控制器u2＝－k2e2，即可实现两个统一混沌系统同步。