基于混沌理论的图像加密研究

图像加密是在密钥和加密算法的共同作用下将一副图像变成杂乱无章的类似于噪声的加密图像，使图像的真实内容无法被非授权用户查看到。与明文图像相比，加密图像的变化表现在三个方面：图像像素的相互位置关系发生了变化，这是由图像像素置乱实现的；图像的像素值发生了变化，使得加密图像的直方图变得平滑，密码分析者很难由加密图像的直方图获取图像的特征；图像相邻像素之间的相关性降低了。

对图像进行加密时，可以借鉴传统的文本加密方法。但图像加密具有一定的特殊性，主要体现在三个方面：首先，由于数字图像包含的数据量大，图像加密速度要快；其次，由于人们对图像信息的损失较为敏感，解密图像的误差要小；最后，因为明文图像相邻像素之间的相关性强，冗余度高，通常需要对整幅图像的图像数据进行加密。近年来，人们根据数字图像的特点，提出了很多图像加密算法，如基于信息熵的图像加密方法、基于像素置换的方法、基于伪随机序列的方法、基于SCAN模式的图像加密方法和基于现代密码体制的方法等。近年来，随着混沌理论与应用的快速发展，研究人员又将目光投向了混沌密码学，并提出了许多基于混沌的图像加密方法。

1998年，J.Fridrich首次将C.E.Shannon的信息安全理论和混沌理论结合在一起应用到数字图像加密算法的设计中，并给出了设计基于混沌理论的图像加密算法的5个基本步骤。在该替代—扩散加密框架的基础上，Lian等提出了一个经典的置乱—扩散框架，框架结构如图1.4所示。

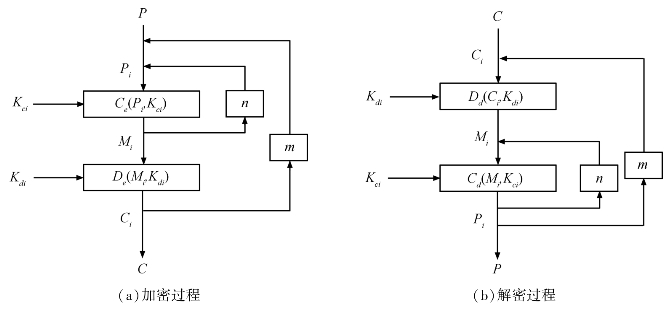
图1.4　Lian等提出的置乱—扩散框架

图1.4中，P和C分别表示明文和密文，Kci为置乱过程的密钥，Kdi为扩散过程的密钥。为了在获得更高的安全性的同时尽量降低计算的复杂性，置乱过程Ce（Pi，Kci）首先执行n次，然后再和扩散过程De（Mi，Kdi）共同执行m次。由于图像中的像素点可以看成二维的像素点矩阵，可以使用二维混沌映射对像素点的位置进行置乱，使用单独的混沌映射完成扩散过程。

在图像置乱过程中，如果采用现有的二维混沌映射，置乱的图像会出现不同的不动点问题。例如，如果使用猫映射进行位置置乱，则图像左上角（0，0）位置的像素点不会改变，当使用面包师映射时，图像左上角（0，0）位置的像素点和右下角（N－1，N－1）位置的像素点同样无效。为了解决这个问题，Lian等对标准映射进行了改进，将一个随机位置（rx，ry）引入置乱操作中，即采用如下公式

当采用标准映射进行迭代前，首先产生一个随机位置（rx，ry），它表示图像中随机选择的像素点的位置。整幅图像向水平和垂直位置分别移动rx和ry，即左上角位于（0，0）位置的像素点被移动到（rx，ry）的位置。

扩散过程De（Mi，Kdi）由一个扩散函数实现，能够将一个像素值的修改扩散到其他的像素值。扩散函数定义为

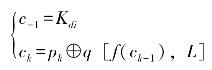
其中，pk为中间密文Mi的第k个像素的像素值，ck为像素替代后的像素值，L为图像像素的灰度级。c－1为扩散函数的初始值，取值为密码系统的密钥。f（·）为Logistic映射，定义为

f（ck）＝4ck－1（1－ck－1）

q（·）为量化过程，定义为

q（X，L）＝2L·X

其中，X＝0.b0b1b2…bL…为X的二进制表示形式，bi为0或1。

理论分析和实验结果表明，Lian等提出的图像加密方案不仅具有较高的安全性，而且具有较低的计算复杂性，在数字图像、音频和视频加密中具有巨大的应用前景。

然而，Wong等在文献中指出Lian等提出的加密方法运行时间过长，要想达到合理的安全级别，至少需要加密的轮数为n＝4和m＝4，即共需要执行16次置乱和4次扩散操作。Wong等分析了Lian等人算法效率较低的原因，即置乱阶段与扩散阶段没有进行适当的融合。为此，黄国和给出了一个改进的加密框架，如图1.5所示。(www.xing528.com)

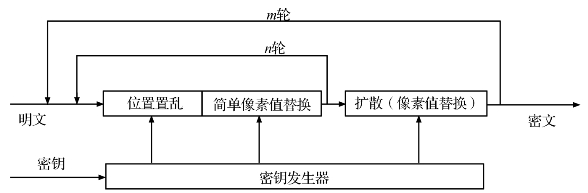
图1.5　Wong等提出的改进加密框架

在图1.5所示的框架中，置乱阶段不再单纯地对像素点的位置进行移动，而是与一个简单改变像素值的操作相结合，即在每一次计算出像素点的新位置之后，对当前像素点的值进行简单的替换，然后再改变下一个像素点的位置。简单像素值替换操作采用了“相加移位”操作，采用如下公式

vi＝Cyc［（pi＋vi－1）mod L，LSB3（vi－1）］

其中，pi为当前处理的明文像素点的值，vi为加密后的像素点的值，L为图像像素的灰度级别，Cyc［s，q］执行对比特序列s右循环移位q比特。LSBk（z）返回z的最低的k个比特。大量实验结果表明，与Lian等提出的图像加密算法相比，Wong等提出的改进算法在达到相同安全性的前提下节省了2／3的时间。

除了基于置乱—扩散框架的图像加密算法，一些专家学者提出基于高维混沌映射的图像加密方法。例如，陈关荣等提出了一个基于三维猫映射的图像置乱算法。在置乱阶段，将原始二维猫映射在3个不同的平面（x－y平面，x－z平面和y－z平面）上扩展成三维。此时，通过每一个平面扩展得到的三维猫映射只有一个平面具有置乱效果。然后将3个三维猫映射结合在一起，得到在3个平面均有置乱效果的三维猫映射，用公式表示为

其中，

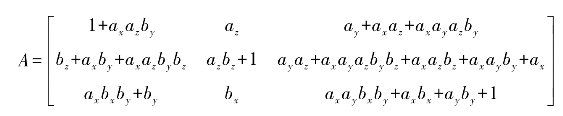
当ax＝bx＝ay＝by＝az＝bz＝1时，改进的三维映射（1.4－2）的3个Lyapunov指数分别为7.184 2、0.243 0和0.572 8，大于二维猫映射，即映射（1.4－2）具有更好的随机性。置乱过程使用的参数｛ax，bx，ay，by，az，bz｝以及扩散过程使用的初始参数均采用Chen系统计算得到，具体的加密框架如图1.6所示。

图1.6　基于三维猫映射的图像加密框架

加密算法首先将二维图像转换成三维，即将二维矩阵转换成一系列的立方体集合，使用公式（1.4－2）对所有的立方体进行置乱。对置乱后的矩阵采用异或并取模的方式进行扩散操作，即采用公式

其中，I（k）为位置置乱后的像素点的值，r（k）为由Logistic映射迭代产生的随机数，其初始值由Chen系统计算产生，c（k）为进行像素值替换后的密文值，N为图像的灰阶。

为了达到更好的加密效果，一些文献将二维猫映射扩展到三维，使得像素点的置乱过程扩展到三维空间，可以进一步降低置乱后相邻像素点之间的相关性。同时，三维猫映射能够带来更大的密钥空间，并使其Lyapunov指数明显提高，从而使得混沌系统对初始值更加敏感。

事实上，有实用价值的混沌图像加密方法必须是针对图像特点的专用方案。混沌图像加密除了可以考虑在空间域上进行，还可以在频率域上进行。空间域图像加密算法能够充分利用图像数据的点阵特征，实现简单，算法直观，加密过程不会引起图像畸变。然而，对于这些图像置乱算法，虽然表面上看密文块是随机的，但这些排列通常是预先确定好的，与密钥无关，容易受到差分攻击。采用频域算法时，频域中每个点的变化都会对整个数据集产生一定的影响，相对于空间域算法，效率和安全性会更高。