计算Lyapunov指数的方法

对混沌判定方法的研究表明，Lyapunov指数是描述混沌现象的重要特征量，也是最能准确判断混沌现象的依据。除了1.1.3节中介绍的根据定义计算Lyapunov指数外，还有很多种计算Lyapunov指数的方法，但其大体上可以分为两类：Wolf方法和Jocobian方法。其中，Wolf方法适用于时间序列无噪声，切空间中小向量的演变呈现高度非线性；Jocobian方法适用于时间序列噪声大，切空间中小向量的演变接近线性。

1.1.4.1　Wolf方法

1985年，Wolf等首先提出直接基于相轨线、相平面、相体积等的演化来估计Lyapunov指数的值。这类方法都是对单变量的时间序列进行相空间重构来提取Lyapunov指数的，这是因为一般的实测时间序列无法确切其代表的原始动力学过程，很难精确地计算出Lyapunov指数值。

Wolf方法是对系统两条或更多条轨道进行跟踪，获得它们的演变规律以提取Lyapunov指数，其基本思想是：

设混沌时间序列为｛x1，x2，…，xk，…｝，嵌入维数为m，延迟时间τ后重构的相空间为Y（ti）＝（x（ti），x（ti＋τ），…，x（ti＋（m－1）τ）），i＝1，2，…，N。取重构相空间的初始点Y（t0），设其最近邻点为Y0（t0），两点之间的距离为L0。追踪这两点的时间演化，直到它们之间的距离超过某个正的规定值ε时，将这一刻时间记为t1，即：L′（t1）＝｜Y（t1）－Y0（t1）｜＞ε，保留Y（t1）的值。接着在Y（t1）附近寻找一个满足L（t1）＝｜Y（t1）－Y1（t1）｜＜ε的点Y1（t1），并且使两者之间的夹角尽可能地小。继续重复上述追踪的过程，直到Y（t）到达时间序列的终点。这时追踪演化过程总的迭代次数为M，则最大Lyapunov指数为：

图1.1描绘了用Wolf方法计算最大Lyapunov指数的整个过程

图1.1　Wolf法求最大Lyapunov指数示意图

如果要计算次大的Lyapunov指数，则要追踪一个点以及邻近两个点构成的三角形的时间演化。如果这个三角形变得太偏斜或者其面积A′（t1）变得太大，需要重新选取一个两边与原三角形两条边夹角最小的三角形A（t1）。重复上述追踪过程，直到终点，则次大的Lyapunov指数λ2满足：

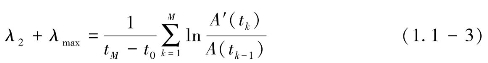(www.xing528.com)

用此方法计算次大Lyapunov指数的示意图如图1－2所示。同理，用此方法可以求得其他的Lyapunov指数。

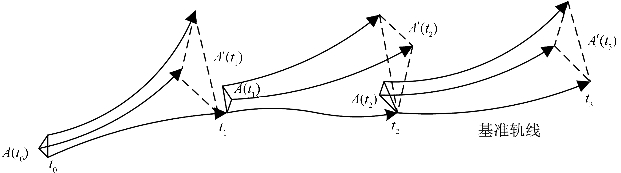
图1.2　Wolf法求次大Lyapunov指数示意图

原则上，对于无噪声的无限长的时间序列，Wolf方法可以精确求得系统所有Lyapunov指数的值。但实际应用中，由于噪声的影响和时间序列长度有限，该方法只能较为可靠地估计其最大Lyapunov指数。

1.1.4.2　Jacobian方法

为了进一步辨别混沌与随机过程，求解Lyapunov指数值是关键。运用Jacobian方法求Lyapunov指数值是一种在实际应用中发展起来的方法，其基本思想为：

设混沌时间序列为｛s1，s2，…，sk，…｝，嵌入维数为m，延迟时间τ后重构的相空间为x（ti）＝（s（ti），s（ti＋τ），…，s（ti＋（m－1）τ），i＝（1，2，…N），其中离散时间间隔为Δt。假设t（t＝kΔt，k∈｛1，2，…，N－1｝）时刻时，点x（t）处的单位切向量为e，经过时间Δt后，切向量演变为e′。在很短的时间内，切向量的演变过程是接近线性的，因此可以用轨道上的点x（t）处的其他切向量的演变值的线性组合来近似代替e的演变值e′。考虑空间中点x（t）到轨道上其他点所形成的小向量xi构成的矩阵X＝（x1，x2，…，xn），xi＝x（liΔt）－x（t），其中要求小向量xi充分小，即｜x（liΔt）－x（t）｜＜ε，li∈｛1，2，…，N｝。

选取一个特定的线性组合y，使其满足条件Xy≈e，y∈Rn。显然，线性组合y经过时间Δt后，使得式子X′y≈e′，y∈Rn成立。其中，X′是由X中的切向量演变而成的向量组。如果前面所述的演变过程具有很好的线性特征，则有Xy≈e和X′y≈e′，其中y＝X＋e，X＋＝（XTX）－1XT。

最后根据Lyapunov指数的计算公式1）Δt‖／‖e（jΔt）‖），得到