1.(1)因为a=10x+y=9x+(x+y),所以9|a⇔9|(x+y).
(2)因为a=10x+y=10(x+2y)-19y,所以19|a⇔19|(x+2y).
(3)因为a=10x+y=10(x+3y)-29y,所以29|a⇔29|(x+3y).
一般地,可猜想并仿上证明,对任意的正整数n,有如下结论成立:
![]()
进一步还可猜想并证明末位是1的数的整除性判别依据:
对任意的正整数n,(10n+1)|a⇔(10n+1)|(x-ny).
进而还可猜想并证明末位是3或7的数的整除性判别依据:
对任意的正整数n,(10n±3)|a⇔(10n±3)|[x±(3n±y)].
2.例如,(57-1)÷2=28在表中,57是合数;(53-1)÷2=26不在表中,53是质数.
观察数表不难发现:第k行与第k列相同,即关于从左上方到右下方的对角线对称.
各行(列)都是等差数列,通项依次为
![]()
上述各式右边前项(表中第1列)成等差数列,通项为4+3(i-1),各式右边后项(j-1)的系数(各行所成数列的公差)又成等差数列,其通项为3+2(i-1).
所以表中位于第i行与第j列交叉处的数为
![]()
显然,aij=aji,这说明表中位于第i行与第j列交叉处的数,等于表中位于第j行与第i列交叉处的数,这与表的构成特点相吻合.
因此,一个正整数a在数表中⇔a=2ij+i+j(i,j∊N*).
进而可得判定定理:正整数a在数表中⇔2a+1为合数(证略).
3.根据“各圆圈内四个数大小须搭配”这一思考目标,通过试验不难得到几个乃至十几个答案(如下图1给出了一个),求全答案步骤如下:
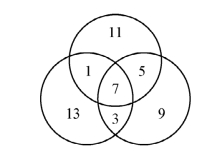
图1

图2
(1)问题代数化.设问题答案如图2所示,且各圈内四数之和为x.
(2)确定x.
(3)依x定g.
(4)依x,g定a,b,c,d,e,f,分类讨论得18个解(见下表).
(5)求全答案:由图1空中可填数的对称性和轮换性可知,对任一独立解,均对应另5种填法,所以,共有18×6种填法.
18个独立解表
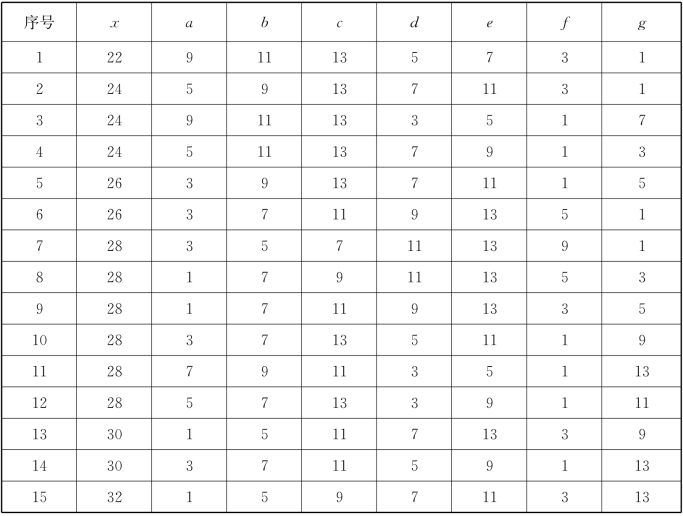
续表

习题2.1
1.(1),(5),(6)成立;(2),(3),(4)不成立.
2.(1)3;(2)6;(3)5;(4)1.
3.(1)√;(2)×;(3)×;(4)√.反例略.
4.略.
5.略.
6.一个数的末3位数字组成的数,能被8或125整除.
7.24,29.
8.1.
9.n=4k+2(k∊N).
10.x=y=4.
11.(1)略;(2)6位能,7位不能.
习题2.2
1.1,3,5,7,9,11,13,15,17.
2.提示:(m-1)2与1同余,来自一类.(https://www.xing528.com)
3.模5的最小非负完全剩余系为0,1,2,3,4;
模5的绝对最小完全剩余系为-2,-1,0,1,2;
一一对应关系:0≡0(mod5),1≡1(mod5),2≡2(mod5),3≡-2(mod5),4≡-1(mod5).
4.提示:利用模m的最小非负完全剩余系0,1,2,…,m-1.
5.提示:设整数n=7m+t(t=-3,-2,…,2,3)证明.
6.80个.
7.31,2.
8.略.
9.7875.
10.略.
习题2.3
1.6.
2.1.
3.84.
4.1.
5.可.
6.略.
7.由费马小定理推论可得.
8.由费马小定理推论可得.
9.略.
10.30.
习题2.4
1.(1)01,0010;(2)9990,99909.
![]()
3.前两个可以分别化为3位和4位有限小数:0.062,0.5968;

5.2160.
6.参照定理3证明.
习题2.5
1.(1)该式不符合同余方程及其解的定义,不在我们讨论的范围.事实上,x可以取任意实数,讨论这样的问题意义不大,故定义将其排除.
(2)唯一.(3)无解.(4)唯一.(5)5个解.
2.(1)x≡5(mod6);(2)x≡0(mod4);(3)2x≡9(mod17);
(4)x≡534(mod2401);(5)x≡200(mod551);(6)x≡81(mod337).
3.(1)2个解为x≡6(mod18),x≡15(mod18).
(2)3个解为x≡2(mod18),x≡8(mod18),x≡14(mod18).
(3)无解.
(4)5个解为x≡200+551k(mod2755),k=0,1,2,3,4.
(5)5个解为x≡3+277k(mod1385),k=0,1,2,3,4.
习题2.6
1.(1)有解;(2)无解.
2.a=7k+1(k是整数)时有解.
3.(1)x≡57(mod504);(2)x≡109(mod440).
4.(1)x≡271(mod360);(2)x≡127(mod216);
(3)x≡107(mod140);(4)x≡73(mod105).
5.17人.
6.至少19袋.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




