2018!的质因数分解结果及唯一性

因为大于1的整数不是质数就是合数，所以定理2给出的质数判定法，也是合数判定法，同时也给出了寻找正整数的质因数的方法.

定义3 把一个大于1的正整数表示成它的质因数之积的形式，叫作把这个正整数分解质因数.

例如，把30分解质因数的结果是2×3×5，或3×2×5，但2×15，5×6不是.

定理4 （算术基本定理)任一大于1的正整数均可分解质因数，而且，如果不计较各质因数的先后次序，其分解结果唯一.

证明 存在性.

若这个大于1的正整数a是质数，作为特例把它自己当作分解结果.

若a是合数，由定理1可知，a至少有一个质因数p1，设a=p1a1（显然a1＞1).若a1是质数，则a=p1a1即为分解结果.

若a1为合数，则a1至少有一个质因数p2，设a1=p2a2（a2＞1)，则a=p1a1=p1p2a2.

再对a2重复上述过程，依此类推下去.

由于a＞1，而a＞a1＞a2＞…，这一过程不可能无限重复下去，设第n-1次结果为a=p1p2…pn-1an-1，且an-1为质数，记pn=an-1，则

即存在质数p1，p2，…，pn-1，pn，使得a可以分解成质因数的乘积.

唯一性.

设a分解质因数的结果有如下两种：

a=p1p2…pn（p1≤p2≤…≤pn，p1，p2，…，pn均为质数)，

a=q1q2…qm（q1≤q2≤…≤qm，q1，q2，…，qm均为质数).

则

不妨设n≤m，则从a=p1p2…pn看，p1是a最小的质因数，从a=q1q2…qm看，q1是a最小的质因数.若p1＜q1，则与q1是a的最小质因数矛盾，若q1＜p1，则与p1是a的最小质因数矛盾，所以p1=q1.

在（※)式中消去p1，q1，得

重复上述过程，可依次得到

而若n＜m，则由（※)式可得1=qn＋1qn＋2…qm，这与qn＋1，qn＋2，…，qm为质数矛盾，所以n＜|m，所以

即a分解结果唯一.

为了应用方便，我们给出标准分解式的概念.

定义4 把大于1的正整数a分解质因数的结果写成如下的形式：

其中p1，p2，…，pn均为质数，且p1＜p2＜…＜pn，α1，α2，…，αn均为正整数，这种分解形式叫作a的标准分解式（以后提到标准分解式，如无特别要求，不再注明条件).

例如，108=22×33是108的标准分解式，而108=33×22不是.

由算术基本定理不难得到下面的结论.

例4 写出7007的标准分解式.

分析 用从小到大的质数2，3，5，…依次试除，为简化书写过程，通常写成大家熟知的短除法的形式.

解

故7007=72×11×13.

下面我们介绍一个有关n!的标准分解式的重要结论.

不超过实数x的最大整数记作[x].例如，[π]=3，[-3.7]=-4.

函数y=[x]，x∊R叫作高斯(Gauss)函数，通常叫作取整函数.这种通常叫法容易使人误解“[x]是x的整数部分”，如误解[-1.3]=-1.

定理5 在n!的标准分解式中，质因数p的指数为

当p≤n时，设想把2，3，4，…，n都分解成标准分解式，由算术基本定理，h就是这n-1个分解式中p的指数之和.

在这n-1个分解式中，设

含因数p的有n1个，共有n1个p；

含因数p2的有n2个，共有2n2个p；

……(www.xing528.com)

含因数pk的有nk个，共有knk个p.

则n!分解式中含有质因数p的次数，就是上述p的个数的总和.

即

其中Nr=nr＋nr＋1＋…＋nk是2，3，…，n这n-1个数中pr的倍数的个数.

于是，在n!的标准分解式中，质因数p的指数为

例5 求2018!的末尾0的个数.

分析 因为10=2×5，所以2018!末尾0的个数相当于2018!的质因数分解式中2×5的个数，由于2＜5，故2018!的质因数分解式中所含2的个数大于5的个数，因此只要考察2018!含有质因数5的个数，即2018!含有质因数5的最高幂指数即可.

解 因为625=54＜2018＜3125=55，所以2018!含有质因数5的最高幂指数为

所以2018!的末尾0的个数是502.

因此，约简后的分母为23·352.

本节结束之前，有必要特别指出：虽然定理4从理论上解决了一个大于1的正整数可以分解质因数而且结果唯一，但实际上当一个正整数比较大时不好分解.

例如，据1994年5月2日《参考消息》第7版刊登的一条消息称：1977年美国数学家和计算机专家发明了RSA密码系统，作为该系统的一个破译难度标准，编制了由两个质数相乘得到的一个129位数构成的密码数，结果经过五大洲600多位科学家用1600台计算机联网，合作攻关8个月才破译，即把这个密码合数分解为两个质数之积.

在现代政务和商务活动中，数字签名就是利用这一原理设置密钥中的公钥和私钥.

关于密码学的更多介绍，请参见本书的附录2.

数论中还有许多类似的问题，看似简单，实则可能是困扰了数学家们几百年的难题.

例如，由上节“2”的性质5与本节质数的概念易知，“两个奇质数之和是一个不小于6的偶数”.反之，其逆命题“一个不小于6的偶数，可以表示为两个奇质数之和”成立吗？

早在1742年6月7日，彼得堡科学院院士哥德巴赫（Goldbach)给大数学家欧拉（Euler)的信中就提出该问题并猜想成立.欧拉当月30日复信断言成立，但又说明自己不能给出证明.

几百年过去了，数学家们一直前赴后继，但至今尚未获证，这就是世界数学史上著名的哥德巴赫猜想(简记为(1+1)).

反证易知，去掉猜想表述中的“奇”字，仍与原表述等价.即，每个不小于6的偶数，均可表示为两个质数之和.

截至目前，最好的成果“每个不小于6的偶数，均可表示为一个质数与不超过两个质数的乘积之和”（1＋2)是由我国数学家陈景润在1966年给出的.

值得指出的是，那之后的几十年来，中科院、大学研究所、报刊社不断收到关于（1＋1)的错误证明，中科院专家告诫人们：“不仅业余爱好者证不出来，就是数论专家在采用新方法之前也不可能得到证明.”（参见2002.10《数学通报》P3《谁在证明哥德巴赫猜想》)

习题1.4

1.使n＋k（k=1，2，3)均为合数，且n＋3≤30的正整数n的允许值有多少个？

2.设a为偶数，且a＞4，p，q均为质数，若a=p＋q，求证：p，q均为奇质数.

3.91个人可否平均分成几个小组？如可，有哪几种分法？

4.36块体积为1的正方体，可拼成几个不同的棱长大于1的长方体？

5.求证：连续4个正整数的乘积与1之和是合数.

6.判断下列各数是质数还是合数：

（1)2641，3848，823，2027；

（2)f（n)=n2＋n＋41（n=39，40).

7.把9个数20，26，33，35，39，42，44，55，91分为三组，每组3个数，使各组内的3个数之积相等.

8.把999999999999分解为标准分解式.

9.某人出生年月日数之积为428575，求此人出生日期.

10.若1176a=b4（a，b为正整数)，求a的最小值.

12.求100!末尾0的个数.

13.写出50!的标准分解式.

14.将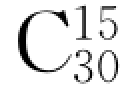分解为标准分解式.