实验成果:斯涅耳发现折射定律

荷兰数学家斯涅耳于1620年前后，通过实验确立了开普勒想发现而没能发现的折射定律。他注意研究了水中的物体看起来像飘浮的现象，做了如下实验：当在空气中的O点观察水中的A点时，犹如在B点一样，如图1所示。斯涅耳发现，对于任意入射角存在以下关系，如图2所示。

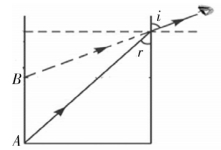
图1　

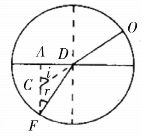
图2

斯涅耳没有用理论推导，而是用实验又验证了它。斯涅耳对折射定律做了如下表述：。(www.xing528.com)

在不相同的介质里，入射角和折射角的余割之比总是保持相同的值。由于余割和正弦互为倒数，所以这个叙述等价于现代折射定律的表达式。

小贴士：折射定律又名斯涅尔定律。设真空光速为c，介质中光速为v，折射率为n，则n=c/v=sin i/sin r。

资料：大约是在1621年，斯涅耳通过实验确立了开普勒想发现而没能发现的折射定律。当时，斯涅耳注意到了水中的物体看起来像漂浮的现象，并试图揭开其中的奥秘。由此便引出了他对折射现象的研究。

在总结托勒密、开普勒等前人的研究成果后，斯涅耳做了进一步的实验。在实验中，斯涅耳应用开普勒的方法发现：从空气到水里并落在容器垂直面上的一条光线在水中所走的长度，同该光线如按未偏离其原始方向而本来会通过的路程成一定的比。他指出：折射光线位于入射光线和法线所决定的平面内，入射光线和折射光线分别位于法线两侧，入射角的正弦和折射角的正弦的比值对于一定的两种媒质来说是一个常数。这个常数是第二种媒质对第一媒质的相对折射率，即：sin i1/sin i2=n21，n21=n2/n1。其中i1和i2分别为入射角和折射角；n21为折射光所在媒质对入射光所在媒质的相对折射率；n2和n1为两种媒质的绝对折射率。斯涅耳的这一折射定律（也称斯涅耳定律）是从实验中得到的，未做任何的理论推导，虽然正确，但却从未正式公布过。只是后来惠更斯和伊萨克·沃斯两人在审查他遗留的手稿时，才看到了这方面的记载。