且不论宗教内部那些奇特的规定，毕达哥拉斯还是非常重视数学的。其程度之深足以让他处死一个门徒，只因其与自己想法不同。我知道下面的这个故事与天文学并没有什么关系，可是毕达哥拉斯实在是个有趣的人。您可以从下面的内容中自己做出判断。
数字在今天对我们来讲，是用于描述某单位内一种抽象连续性的术语。如，什么是“3”？这是一个比“2”大一些的数字。这个逻辑关系适用于任何数字。
然而，毕达哥拉斯并不这样看待数字。他认为重要的是数字之间的关系，如3和2的关系与6和4的关系相同。因为这两组数字做除法的结果都是1.5。
需要注意的是，如今普遍使用的数字直到12世纪才由阿拉伯人发明出来[1]。虽然我们可能没有意识到，不过这一发明确实大大促进了整个人类社会的发展。而且，在古希腊时代，人们还没有接触过“零”这一概念。
在毕达哥拉斯那个时代，想要尝试使用希腊字母像如今一样去研究数学问题是不可能的，于是他们设计出“几何”这种更加直观的方式来研究数学。
如果您对学生时代的课程还有一些模模糊糊的印象，那您应该会记得勾股定理，即在一个直角三角形中，斜边的平方等于其他两边的平方的和。如下图，也可以表达为：a2 + b2 = c2。
如果想计算三角形斜边的长度，只需要分别计算出另外两条边的平方然后相加再开方即可。而计算平方数对于我们仅仅意味着同一个数字相乘。然而，对那个时代的人来说，他们需要构建一个以三角形一边的长度为边长的正方形，然后去计算其内部的小单位数量。
勾股定理（事实上，并无法考证是毕达哥拉斯本人的理论还是其门徒的研究成果）是一个几何等价定理，即可以被理解为如果用直角三角形的三个边分别组成三个正方形，那么两个较小的正方形面积之和等于大正方形的面积。
这个定理在部分问题的解决上十分有效，然而也给毕达哥拉斯带来了其他的烦恼。
对于较短的两边长度不同的直角三角形来说，应用这个定理是没有问题的。不过若是该直角三角形相交于直角的两边长度相同时就会有一些复杂。尤其是当两边的长度为“1”时，对角线的长度又该如何计算呢？毕达哥拉斯的门徒西帕索斯计算出12+12=C2，那么C=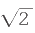
。那时的人们还不懂得，2的平方根是一个无理数，这意味着它的数值是一个无限连续且不会重复的小数：1.41421356 ……
回归正题，毕达哥拉斯并不喜欢十进制数字，他知道可以用整数之间做除法（分数）来表示。
比如，1.5可以表示为3除以2，0.1823相当于1.823除以10。
毕达哥拉斯一定这样想：“虽然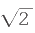
不是整数，但是世界的法则如此，一定存在两个整数，其分数关系可以表达
。”
然而，西帕索斯从数学的角度上（不对，那时应该说是从几何学的角度上）证明了并没有任何两个数字的分数关系可以表达2的平方根。震怒过后，毕达哥拉斯采取了一个完全违背科学的方式来处理这一状况：处死那个持有相反意见的人。就这样，他用最为激烈的方式给这个问题画了上句号。
现在，我对毕达哥拉斯这个人已经有点好感了，下面我们继续聊聊天文学。
由于毕达哥拉斯将自己的学校视为一个神秘的社会组织，我们很难找到关于其本人和教众们的实证性材料。杨布里科斯是一位生活在距离毕达哥拉斯750年后的古希腊思想家，他复原了一些当时宗教内部口授笔传的规定，比如，毕达哥拉斯教派的信徒们必须：(www.xing528.com)
放弃使用动物皮毛作为蔽体的衣物；
禁止焚化死者的尸体；
不得烧烤或水煮食物；
在庆典期间不能剪指甲或剪头发；（尽管随着时间推移节日中的习俗多发生了很大变化，可是这一点大家还是会受到毕达哥拉斯教派的影响。）
不得以众神的名义宣誓；
用金子或盐水来清洗献祭仪式中被动溢出的血液。
不知道您有没有尝试过用对折的纸张来清理溢出的液体，这的确让人无从下手。我真的无法想象那些门徒如何使用黄金这样根本不吸水的材料来清理血液，这简直是个灾难。
毕达哥拉斯与一众门徒都非常重视身体和精神的营养摄取。关于他们的饮食结构，可以阅读古代哲人撰写的文献。有人说毕达哥拉斯是绝对的素食主义者，因为他相信轮回，吃肉则与谋杀无异。而亚里士多德认为宗教的规定只是限制食用动物的某些部位，如心脏或胎盘。（动物的胎盘很美味么？）
不过，几乎所有人都认为毕达哥拉斯对豆子有着一种常人不太理解的恐惧。他的教会学校不允许食用豆子，甚至也不可以从播种了豆子的土地上经过。
没人知道，为什么毕达哥拉斯会有这种抗拒豆子的怪癖，而亚里士多德在谈论毕达哥拉斯教派时，曾经解释过一些可能的成因：
● 他们之所以认为豆子具有毁灭性，可能是因为食用豆子后胃胀气的声音和味道会扰乱精神的平和。
● 豆荚的形状类似生殖器，而且在豆子被咀嚼过后或在阳光下放置一段时间后，味道非常难闻。也有的说法是，它酷似没有铰链的地狱之门，又像皇冠上的宝石，吃豆子就如同在啃食父亲的头骨。这最后一个理由无法通过任何审慎的逻辑来解释，可能是来自毕达哥拉斯教派奇异的想法。
就这样，由于毕达哥拉斯对豆类的恐惧，甚至有传闻称，在敌军入侵克罗托内时，他由于在逃亡途中拒绝穿过一片种植豆类的农田而惨遭杀害。
[1] 阿拉伯数字，最初由古印度人发明，后由阿拉伯人传入欧洲，之后由欧洲人将其现代化。只是，人们以为这些数字是由阿拉伯人发明的，所以称其为“阿拉伯数字”。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
