高压旋喷钢管混凝土桩在深厚软土填石复杂地基中的应用研究

在对桩基的研究中，最主要的内容是桩基的承载力与沉降计算。在过去漫长的时间里，工程师们为了精准和预测桩基沉降，曾做过大量的研究，提出一系列的桩基沉降计算方法，但由于地下桩基础的复杂性以及地基土的不均性，桩基的计算理论还有待进一步成熟。

工程上在选择桩基沉降计算模式以及相应的计算参数时，需要根据荷载特点、土层条件、桩的类型来选择。计算出的结果与实际是否相符很大程度与计算参数的选取正确与否有关。

目前单桩沉降计算方法主要包括荷载传递法、剪切位移法、弹性理论法、分层总和法（建筑桩基技术规范方法）、简化方法（我国路桥规范简化计算法）以及数值计算法。

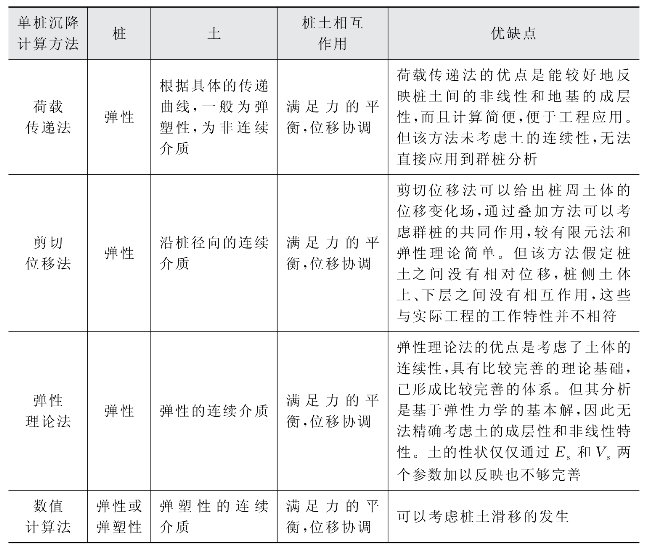
现将各种方法中对桩模型、土模型的假设条件及桩土相互作用模型对比列于表5-1中。

表5-1　单桩沉降计算方法比较

1.荷载传递法

1）荷载传递法的基本原理

荷载传递法是目前应用最为广泛的简化方法，该方法的基本思想是把桩划分为许多个弹性单元，每一单元与土体之间用非线性弹簧连接（图5-2），以模拟桩-土间的荷载传递关系。桩端处土也用非线性弹簧与桩端联系，这些非线性弹簧的应力-应变关系，即表示桩侧摩阻力τ（或桩端抗力σ）与剪切位移s间的关系，这一关系一般称作传递函数。

2）荷载传递法的假设条件

荷载传递法把桩沿桩长方向离散成若干个单元，假定桩体中任意一点的位移只与该点的桩侧摩阻力有关，用独立的线性或非线性弹簧来模拟土体与桩体单元之间的相互作用。该方法是由Seed（1957）提出的。在结合土力学和高等数学知识的基础上，分析桩的受力特点，从理论上建立了桩在竖向荷载作用下桩侧受力的徽分方程，表示如下：

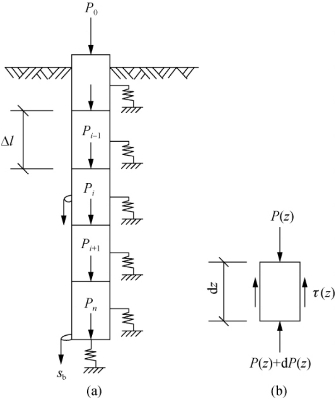
图5-2　桩土共同作用模型　

式中　Ap——桩的截面积（m2）；

Ep——桩的弹性模量（kPa）；

s——桩土相对位移（m）；

z——桩长（m）；

U——桩的截面周长（m）；

τ（z）——桩侧摩阻力沿桩长方向上的分布函数。

3）荷载传递法的求解方法

目前荷载传递法的求解有三种方法：解析法、变形协调法和矩阵位移法。

解析法由Kezdi（1957）、佐藤悟（1965）等提出，把传递函数简化假定为某种曲线方程，然后直接求解。Coyle（1966）提出了迭代求解的位移协调法，曹汉志提出了桩尖位移等值法，这两种变形协调方法可以很方便地考虑土体的分层性和非线性，因此应用比较广泛。矩阵位移法（费勤法，1983）实质上是杆件系统的有限单元法。

常见的荷载传递函数形式如图5-3所示。

考虑桩土软化的桩侧传递函数的三折线统一模型。

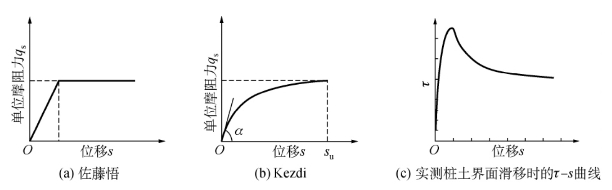
图5-3　传递函数的几种形式

侧阻传递函数模型如图5-4所示。桩侧土的荷载传递函数可统一表达为

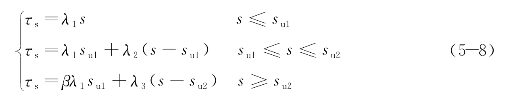
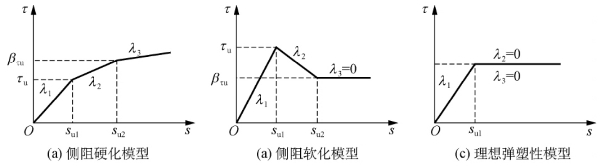
图5-4　侧阻三折线统一模型

式中　τs——桩侧摩阻力（kPa）；

s——桩身相邻的土结点的位移（m）；

λ1，λ2——桩侧土弹性阶段和塑性阶段（硬化或软化）的剪切刚度系数（kPa/m）；

su1——弹性阶段和塑性阶段的界限位移（m）；

su2——弹性阶段和滑移阶段的界限位移（m）；

β——强度系数。

由模型可得

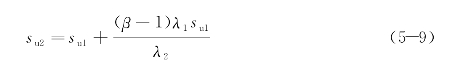
2.剪切位移法

剪切位移法是假定受荷桩身周围土体以承受剪切变形为主，桩土之间没有相对位移，将桩土视为理想的同心圆柱体，剪应力传递引起周围土体沉降，由此得到桩土体系的受力和变形的一种方法。

图5-5所示为单桩周围土体剪切变形的模式，假定在工作荷载下，桩本身的压缩很小可忽略不计，桩土之间的黏着力保持不变，亦即桩土界面不发生滑移。(www.xing528.com)

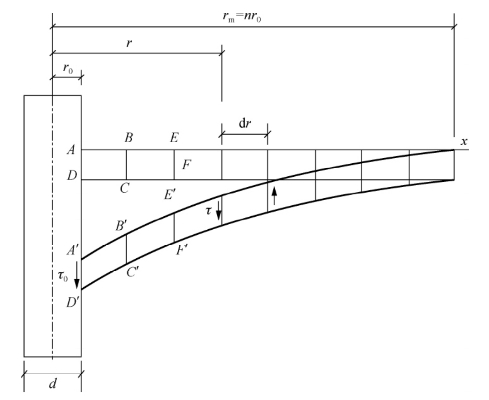
图5-5　剪切变形传递法桩身荷载传递模型

在桩土体系中任一高程平面，分析沿桩侧的环形单元ABCD，桩受荷前ABCD位于水平面位置，桩受荷发生沉降后，单元ABCD随之发生位移，并发生剪切变形，成为A′B′C′D′，并将剪应力传递给邻近单元B′E′C′F′，这个传递过程连续地沿径向往外传递，传递到x点距桩中心轴为rm＝nr0处，在x点处剪应变已很小可忽略不计。假设所发生的剪应变为弹性性质，即剪应力与剪应变成正比关系。

3.弹性理论法

弹性理论法用于桩基的应力和变形计算是20世纪60年代初期提出来的，Poulos，Davis和Mattes等人做了大量的工作。

他们的基本思路是：为了对桩土性状作系统化的分析，首先将实际问题予以理想化，并使它成为数学上容易处理的模型。当这个简单模型的数学性状获得经验之后，就可以将这个理想化模型不断改进，使之更加趋近于实际问题。

Poulos等人所考虑的最简单问题是均质的、各向同性的半无限弹性体重的单个摩擦桩，从这个基本点出发，对问题的理想化加以改进。

弹性理论法的假设条件：弹性理论法假定土为均质的、连续的、各向同性的弹性半空间体，土体性质不因桩体的存在而变化。采用弹性半空间体内集中荷载作用下的Mindlin解计算土体位移，由桩体位移和土体位移协调条件建立平衡方程，从而求解桩体位移和应力。

所有n个单元的应力和桩端应力使单元i处的土产生的竖向位移为

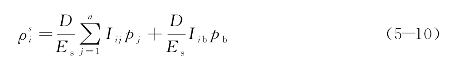
式中　Iij——单元j的剪应力pj＝1时在单元i处产生的土的竖向位移系数；

Iib——桩端应力pb＝1时在单元i处产生的土的竖向位移系数。

4.路桥桩基简化方法

根据当地的特定地质条件和桩长、桩型、荷载等，经过对工程实测资料的统计分析可得出估算单桩沉降的经验公式。由于受具体工程条件限制，经验公式虽然具有局限性，不能普遍采用，但在当地很实用，可以比较准确地估计单桩沉降，并可供其他地区作比较与参考。

《铁路桥涵设计规范》（TBJ 2—85）和《公路桥涵地基与基础设计规范》（JTJ 024—85）中计算单桩沉降s0的公式如下：

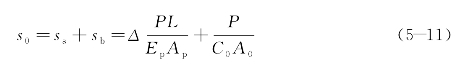
式中　P——桩顶竖向荷载（kN）；

L——桩长（m）；

Ep——桩弹性模量（kPa）

Ap——桩截面面积（m2）；

A0——自地面（或桩顶）以角扩散至桩端平面处的扩散面积（m2）；

Δ——桩侧摩阻力分布系数，对于打入式或振动式沉桩的摩擦桩，Δ＝2/3，对于钻（挖）孔灌注摩擦桩，Δ＝1/2；

C0——桩端处土的竖向地基系数，当桩长L＝10m时，取C0＝Lm0，其中m0为随深度变化的比例系数，根据桩端土的类型选取。

5.单桩沉降计算的分层总和法

单桩沉降分层总和法计算公式如下：

假定单桩的沉降主要由桩端以下土层的压缩组成，桩端摩阻力以扩散角向下扩散，扩散到桩端平面处用一等代的扩展基础替代，扩展基础的计算面积为Ae（图5-6）。

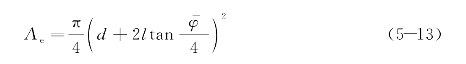
式中，φ-为桩侧各层土内摩擦角的加权平均值。

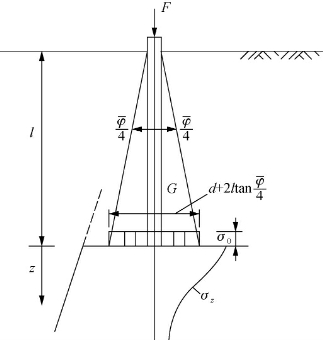
图5-6　单桩沉降的分层总和法简图

6.单桩的数值分析方法

目前应用较为广泛和成熟的数值分析方法主要包括有限元法、边界元法和有限条分法。

1）单桩的有限元法

有限元法是适应计算机而发展起来的一种比较新颖和有效的数值计算方法，随着计算机的发展，有限元的应用越来越广泛。

有限元分析可分为前处理、处理、后处理三个阶段。前处理是建立有限元模型，完成单元网格划分；后处理是采集分析结果，使用户能简便地提取信息，了解结果。

2）边界元法

边界法亦称积分方程法，是一种把区域问题转化为边界问题求解的离散方法，即将筏板地基中的桩进行离散化分析。Banerjee（1969，1976，1978），Butterfield（1970，1971），Wolf（1983）先后用边界元法对单桩和群桩进行分析。

单纯的边界元法假设桩土界面位移协调，没有考虑桩土界面土的屈服滑移，与实际工程有一定差距。Sinha（1966）提出了一种完整的边界元法，把桩离散用边界元法分析，用薄板有限元分析筏板，土被假定为均质弹性体，引入了土的滑移现象，以分析土体的膨胀或固结效应。

3）有限条分法

有限条分法首先用于分析上部结构，并取得成功。Cheung（1976）首先提出将有限条分法用于单桩分析，以分析层状地基中单桩的特性。随后Guo（1987）将有限条分法发展成为无限层法，分析了层状地基中的桩基础，能更有效地求解层状地基中桩与土体的相互作用。王文和顾晓鲁（1988）进一步以三维非线性棱柱单元模拟土体，将桩土地基分割成一些列横截面为封闭或单元敞开的有界或无界棱柱单元，利用分块迭代法求解桩-土体系。