随着桩基理论的发展,各项技术指标已经相当成熟,对大部分桩而言这些理论都有通用性与普遍适用性。对高压旋喷钢管混凝土桩而言,这些理论同样也适用。对于桩基设计而言单桩在竖向荷载作用下的受力性状研究是基础。在不同工程中,地质条件、施工工艺、桩的类型、桩基规范有所不同,桩基的承载受力也有所差别,但其荷载传递机理是相同的:在竖向荷载的作用下,桩受力导致桩身发生相应的压缩变形,桩身与桩周土间产生相对位移,在土体与桩的接触面上产生阻止这一位移的桩侧摩阻力(根据产生相对位移的不同分为正摩阻力和负摩阻力)。若桩侧摩阻力不能完全阻止这种竖向变形,则桩底将承受一部分竖向荷载,桩底的持力土层会产生压缩变形,桩底持力层变形将产生桩端阻力。桩最终通过桩侧摩阻力和桩端阻力将荷载传递给周围土体,起到承载和阻止上部结构沉降的功能。若桩体长度有限,其桩侧摩阻力和桩端阻力是在桩顶部受到外力的一瞬间产生的,可被认为是同时产生、同时结束,二者之间不存在一个异步过程。在计算桩体极限承载力时,对时间可以不予考虑,仅需把桩侧摩阻力和桩端阻力叠加就行。当上部荷载较小时,一般按照弹性公式计算桩的承载力,而不必考虑桩体和土体的塑性变形理论。桩身应力和位移的变化规律也是基于此来进行研究的。基桩的受力性状主要体现在两个方面:基桩竖向承载力和竖向沉降。这两个方面彼此联系,又有区别。
根据桩的荷载传递形式,按桩侧摩阻力和桩端阻力在桩承载力中控制的比例,分为摩擦性桩和端承桩。
根据静力平衡关系,得到公式(5-1):
Q=Qs+Qp(5-1)
式中 Q——单桩桩顶轴力(kN);
Qs——桩侧总阻力(kN);
Qp——单桩桩端总阻力(kN)。
把桩沿着桩长方向分成若干个独立单元,每个单元的位移对应该点的桩侧轴力和摩阻力,得到桩的荷载传递图,如图5-1所示。
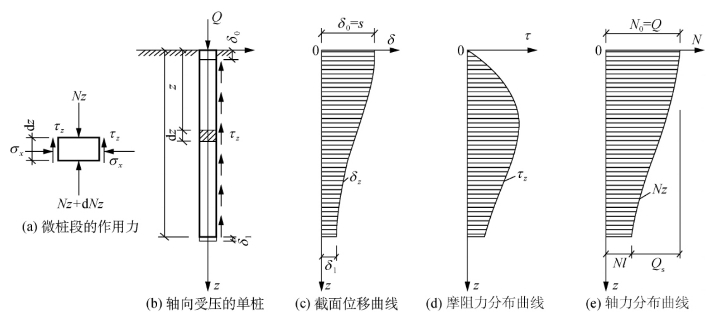
图5-1 单桩轴向荷载传递
荷载传递基本方程的建立如下:
取深度z处的徽小桩端为对象,由力的平衡条件:
Nz-τzupdz-(Nz+dNz)=0
提取τz,得

由力的平衡条件:(https://www.xing528.com)
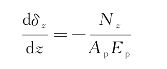
得到z界面荷载:

将式(5-3)代入式(5-2)中得

任一深度z处的桩身轴力、桩身截面位移:
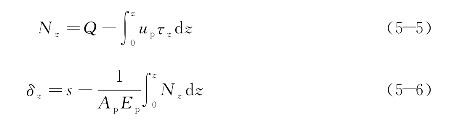
式中 τ——桩侧摩阻力(kPa);
δ——桩土相对位移(m);
Ap——桩的横截面积(m2);
Ep——桩身弹性模量(kPa);
up——桩身周长(m)。
式(5-1)即反映桩端阻力和桩侧摩阻力同时提供反力阻止桩基下沉。但桩相对于桩周土的位移在桩端和桩侧不是同时发生的,而是从桩侧上端到下端逐步传递,桩周土的摩阻力也是从上到下逐步发挥的。当桩端阻力开始发挥时,桩端会产生较大的位移,这个位移值比桩侧摩阻力达到的最大位移值要大。
荷载传递机理公式阐述了桩侧摩阻力、轴力传递函数、每个断面沉降之间的关系。由式(5-2)可知,在轴力Nz已知的情况下,桩侧摩阻力沿桩深的分布函数可通过轴力Nz的一次积分得到。由式(5-3)可以看出,在已知桩侧摩阻力分布函数时,只需对其积分就可求得桩轴力沿桩身的分布函数。根据式(5-6),由桩轴力分布函数即可求得每个断面的沉降位移。桩的侧摩阻力与桩截面沉降的关系可由式(5-4)(即荷载传递函数)建立。桩的荷载传递函数仅阐述了桩的荷载传递机理,但并不准确描述以及计算一种桩型沉降以及承载力,针对不同的土层、不同的桩型,在计算桩基沉降以及荷载时需要在此荷载传递函数上进一步研究与创新。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




