EV3机器人搭建趣味跷跷板

人们从远古时代起就会使用杠杆，并且懂得巧妙地运用杠杆。在埃及造金字塔的时候，奴隶们就利用杠杆把沉重的石块往上撬；造船工人用杠杆在船上架设桅杆；人们用汲水吊杆从井里取水等，都是利用了杠杆的原理。但是，杠杆为什么能做到这一点呢？

古希腊科学家阿基米德经过反复地观察、实验和计算，终于确立了杠杆的平衡定律（图5-1）。他还曾经说过这样的豪言壮语：“给我一个支点，我就能撬起地球！”今天我们要搭建的跷跷板就和杠杆原理有关。

图5-1 阿基米德与杠杆原理

知识

一、认识跷跷板

1.各式各样的跷跷板（图5-2）

图5-2 各式各样的跷跷板

图5-2 各式各样的跷跷板（续）

2.跷跷板的原理

跷跷板主要是利用了杠杆原理。杠杆原理亦称“杠杆平衡条件”，要使杠杆平衡，作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等（图5-3）。

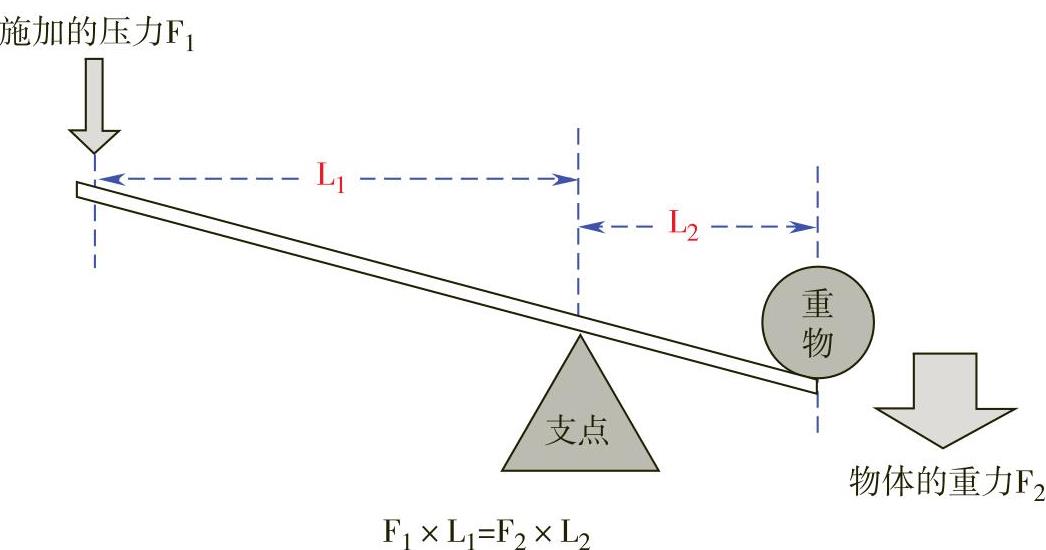
图5-3 杠杆平衡条件

人对跷跷板的压力是动力和阻力，人到跷跷板的固定点的距离均为力臂，重力加速度导致一上一下，高者重力加速度要大于低者，所以高者下降，同时在杠杆原理作用下将低者翘起来，如此循环（图5-4）。

二、LEGO EV3零件介绍

图5-4 跷跷板中的杠杆原理

十字形连接器（图5-5），也叫正交连接器，在搭建中，使用它可以改变轴的连接方向，从而实现轴与梁正交垂直连接。

图5-5 十字形连接器

实践

1.任务要求：制作一个“跷跷板”模型

（1）主体结构坚固、稳定。

（2）模型设计合理、美观。

（3）能够直立于桌面上。

2.准备材料（图5-6）

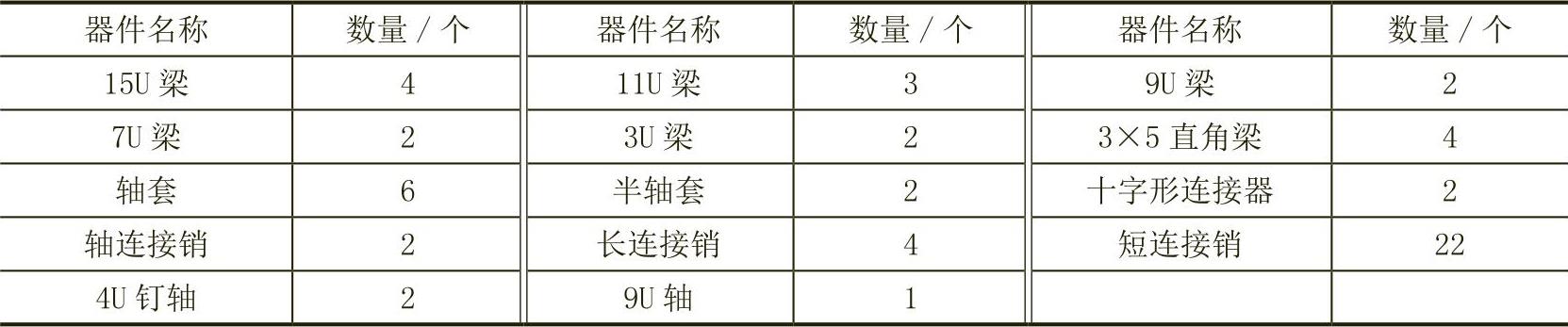
图5-6 准备材料

3.动手搭建

图5-7

第一步：取9U梁2根，7U梁2根，用连接销连接，完成2组，如图5-7所示。

图5-8

第二步：取15U梁2根，与9U梁连接，如图5-8所示。(www.xing528.com)

图5-9

第三步：取11U梁1根，将上一步成品翻过来，与15U梁连接使其稳定，如图5-9所示。

图5-10

第四步：取11U梁2根，将上一步成品翻过来，用短连接销与15U梁连接，完成2组，如图5-10所示。

图5-11

第五步：取15U梁2根，3U梁2根，与连接销连接，分别完成2组，如图5-11所示。

图5-12

第六步：将上一步的2组成果连接在一起，如图5-12所示。

图5-13

第七步：取3×5单弯梁4根，与长连接销相连，完成靠背，如图5-13所示。

图5-14

第八步：用4U钉轴和轴套固定靠背，如图5-14所示。

图5-15

第九步：用9U轴、轴套、半轴套固定跷跷板，如图5-15所示。

图5-16

第十步：将十字型连接器与轴连接销连接，完成2组，如图5-16所示。

图5-17

第十一步：将十字型连接器与9U轴相连，两个十字型连接器的左右方向一致，如图5-17所示。

图5-18

第十二步：将上一步成果与底座相连，完成作品，如图5-18所示。

回顾

开动脑筋，完成本课任务：

（1）在制作跷跷板的过程中，你遇到了哪些困难？你是如何解决的？

（2）如何让平行四边形具有稳定性？

拓展

联想生活中所见到过的各种类型的跷跷板，结合本课知识，自己动手搭建有特色的跷跷板吧！