汽车NVH性能开发：模态贡献量分析结果

在模态分析中得到的特征值是相互独立的，可以任意正规化。哪个模态在结构中起主要作用很难判断，除非进行各种载荷的瞬态响应和频率响应分析。这样一来，无疑会增加计算时间和成本。

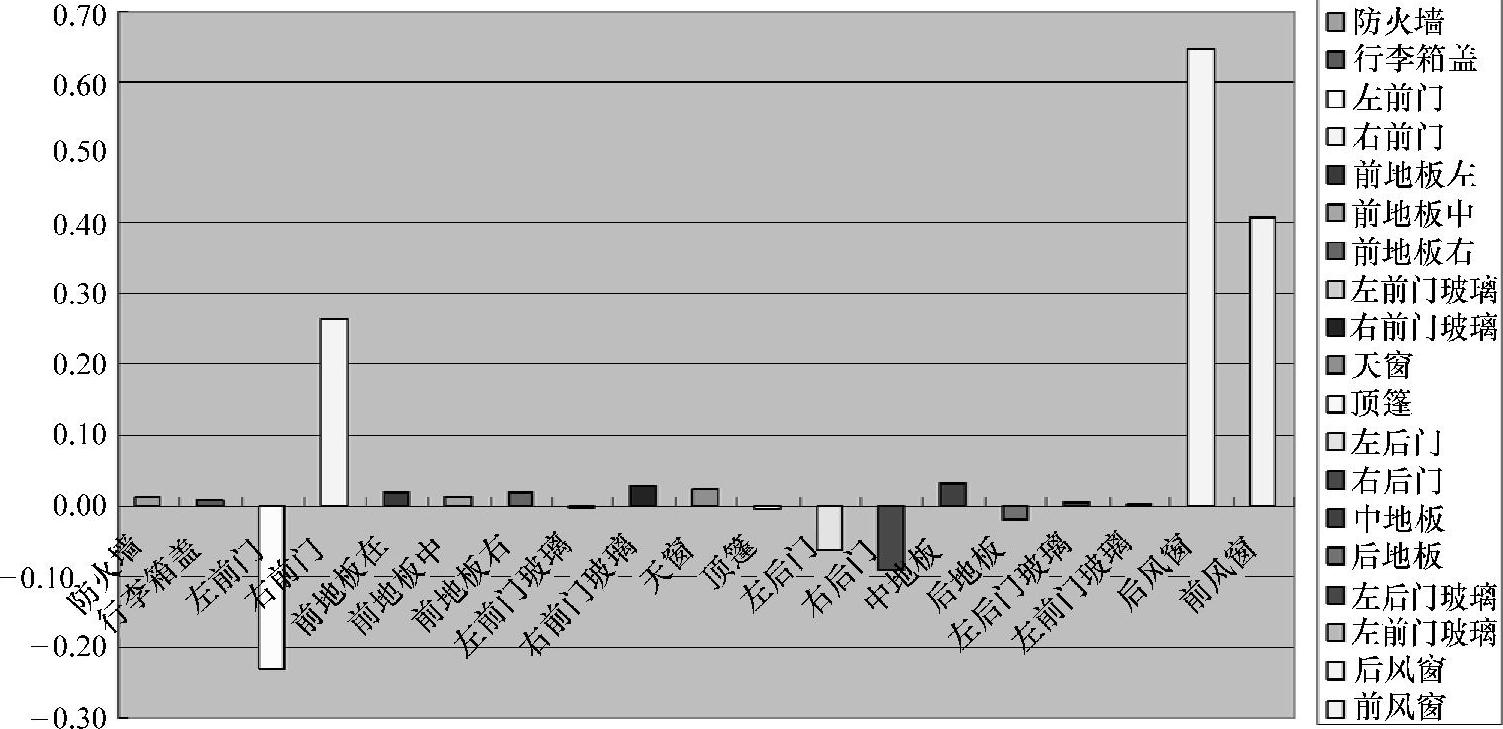
图6.7.2 板件贡献量结果

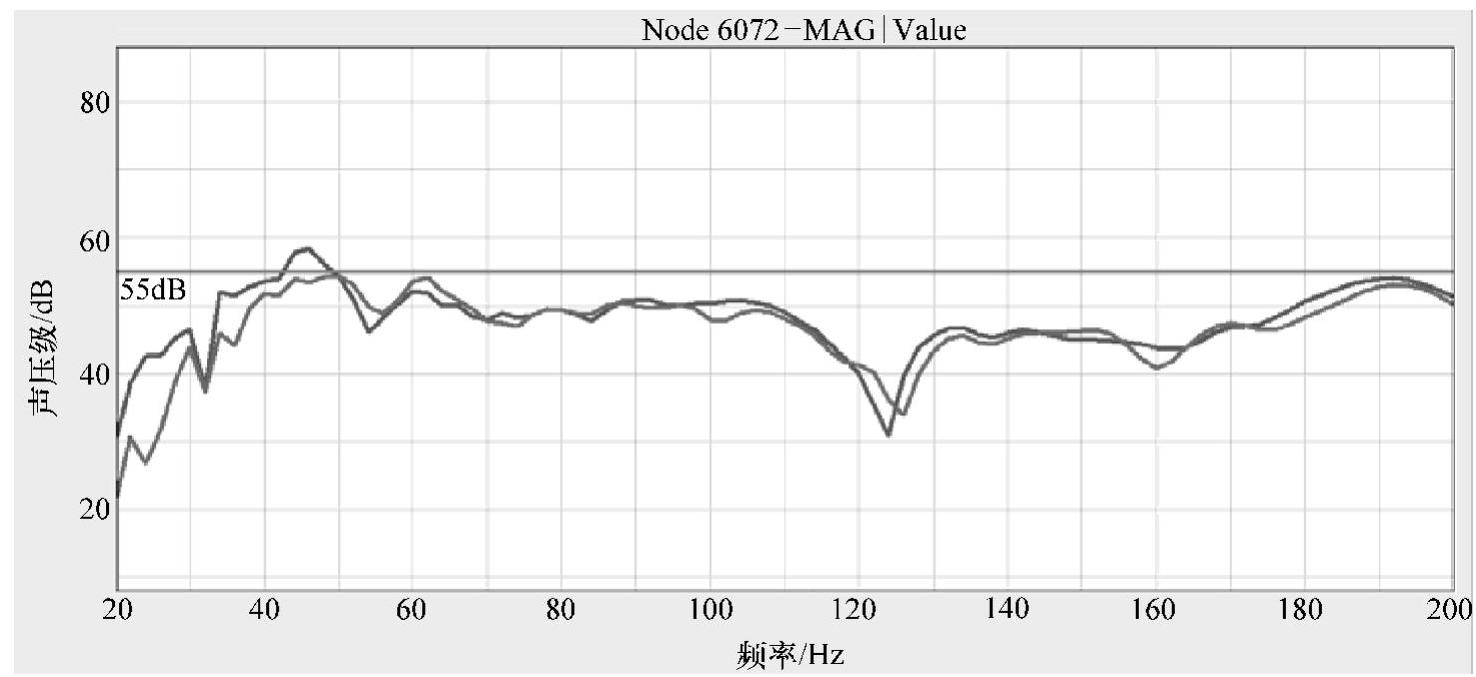
图6.7.3 优化结果

帮助我们判断哪个是重要模态的一个有效方法是模态贡献量分析，也称为模态参与因子分析。

线性特征向量的组合能得到任意的形状。在这种情况下，我们说形成的这个形状是感兴趣响应方向上的一个刚体向量。假设这个刚体向量V_R为

V_R=Φ{ε} （6.42）

式中，ε是向量因子，也就是一系列的参与因子。

左乘Φ^TM，则可以得到：

Φ^TMV_R=Φ^TM{ε}=M_ii{ε} （6.43）

式中，M_ii为每个模态的广义质量对角矩阵；Φ^TMV_R为参与因子；ε是广义质量M_ii的系数，以完成参与因子。

还可以使用相似的方法定义刚体质量M_r，它与模态质量的关系为

M_r=V^T_RMV_R （6.44）(www.xing528.com)

但是

V_R=Φ{ε} （6.45）

所以

M_r=ε^TΦ^TMΦε=ε^TM_iiε （6.46）

每个模态刚体质量M_r的贡献量为

M_r=ε²_iM_ii （6.47）

这就是模态的有效质量。如果质量矩阵正规化：

Φ^TMΦ=[I] （6.48）

参与因子就是ε，模态有效质量就是ε²。

可以在工况控制卡片里加入如下命令来输出模态参与因子。

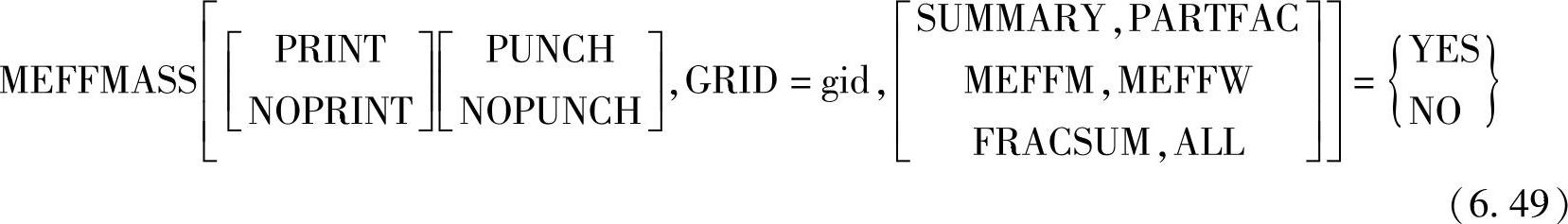
式中，PRINT为输出到f06文件中（默认项）；NOPRINT为不输出到f06文件中；PUNCH为输出到punch文件中；NOPUNCH为不输出到punch文件中；gid为计算质量矩阵的参考节点；SUMMARY为请求计算总有效质量系数、模态质量矩阵和A集中的刚体质量矩阵；PARTFAC为请求计算模态参与因子；MEFFM为请求计算对质量规一化的模态有效质量；MEFFW为请求计算对重量规一化的模态有效质量；FRACSUM为请求计算模态有效质量系数。