汽车NVH性能开发：模态法瞬态响应分析

模态法瞬态响应分析利用结构振型缩减来求解运动方程，比数值求解法效率更高。为了求解运动方程，需要作如下假设：

图6.5.1 初始位移和初始速度定义卡片

{u（t）}=[ϕ]{ξ（t）} （6.30）

上述假设可以将变量从物理空间转换到模态空间。如果使用所有的模态，则上式为等效变换，如果只使用一部分模态，则上式为近似转换。实际中基本上都属于后者。

对于无阻尼运动，则运动方程式为

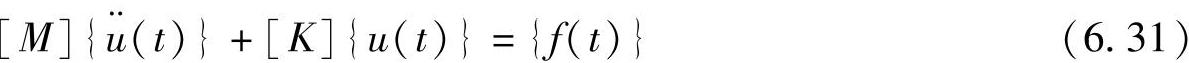
将式（6.30）中的模态坐标代入到式（6.31）中，则可以得到下式：(www.xing528.com)

[M][ϕ]{ξ（t）}+[K][ϕ]{ξ（t）}={f（t）} （6.32）

这就是模态空间中的运动方程式。为了解耦该运动方程，前乘[ϕ]^T，则得到：

[ϕ]^T[M][ϕ]{ξ（t）}+[ϕ]^T[K][ϕ]{ξ（t）}=[ϕ]^T{f（t）} （6.33）

式中，[ϕ]^T[M][ϕ]为模态质量矩阵；[ϕ]^T[K][ϕ]为模态刚度矩阵；[ϕ]^T{f（t）}为模态力。

最后，利用振动的正交特性，用模态质量矩阵和模态刚度矩阵来表达运动方程式，这两个矩阵均为对角矩阵，非对角元素均为零，这时的运动方程不是耦合的。这样一来，运动方程式可以改写为一系列非耦合自由度系统。

m_iξ_i（t）+k_iξ（t）=f_i（t） （6.34）

式中，m_i为第i阶模态质量；k_i为第i阶模态刚度；f_i为第i阶模态力。