汽车NVH性能开发：直接法瞬态响应分析成果

直接法瞬态响应分析中，直接用数值积分方法求解耦合运动方程式。运动方程式如下：

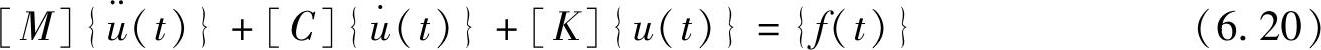
以固定时间步长Δt求出离散点的响应，用中心差分法求解节点处的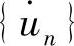速度和加速度：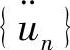

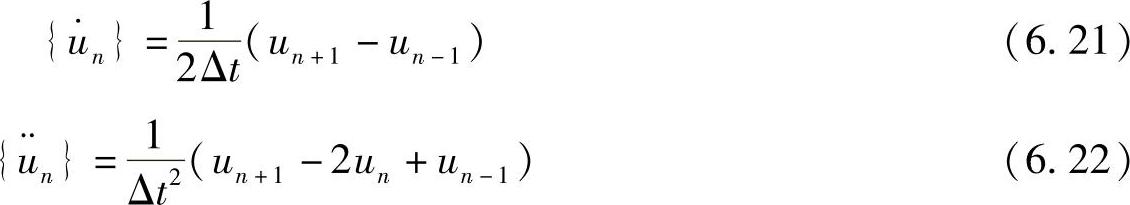
使用Newmark-Beta方法转化为

对上式进行整理，同类项合并，则运动方程式变形为

[A₁]{u_n+1}=[A₂]+[A₃]{u_n}+[A₄]{u_n-1} （6.24）

式中的各系数A₁、A₂、A₃、A₄的意义如下：(www.xing528.com)

上式中，[A₁]称为动力矩阵，[A₂]称为激励矩阵，取三个相邻点的平均值。[A₃]、[A₄]为初始边界条件，取决于上一步的计算结果。

直接瞬态响应分析中的阻尼矩阵由以下几部分构成：

式中：[C₁]为阻尼单元CVSIC或CDAMPi，以及直接输入矩阵C2GG；[C₂]为直接输入矩阵C2GG以及传递函数；G为总结结构阻尼系数；W₃为感兴趣的频率，用于将总体结构阻尼转换为等效黏性阻尼，通过语句PARAM、W₃、n实现，n为转换系数；[K]为总体刚度矩阵；G_E为单元结构阻尼系数，通过MATi卡片的G_E值定义；W₄为感兴趣的频率，用于将单元结构阻尼转换为等效黏性阻尼，通过语句PARAM、W₄、n实现，n为转换系数；[K_E]为单元刚度矩阵。

直接法瞬态响应分析不允许存在复数系数，因此，必须将结构阻尼转化为等效黏性阻尼。上式中的W₃、W₄就是为了阻尼转化而设计的参数。

直接法瞬态响应分析必须定义初始位移和速度。卡片TIC用来定义这些初始条件，如图6.5.1所示。

卡片的第5栏U0定义初始位移，第6栏V0定义初始速度。