直接法频率响应分析-汽车NVH性能开发

1.直接频率响应分析中的阻尼

直接频率响应分析中的阻尼用阻尼矩阵[C]表示，合并在刚度矩阵[K]当中。阻尼矩阵由几个分块矩阵组成：

[C]=[C¹]+[C²] （6.7）

式中，[C¹]为阻尼单元（CVISC、CDAMPi）和C2GG直接输入矩阵；[C²]为C2PP直接输入矩阵和传递函数。

在频率响应分析中，PARAM、G和MATi卡片的GE区域并不形成阻尼矩阵，而形成如下的复数刚度矩阵：

[K]=（1+iG）[K]+i∑G_E[K_E] （6.8）

式中，[K]为总体刚度矩阵；G为总体结构阻尼系数，由PARAM、G的值决定，如PA_- RAM，G，0.16，表示结构阻尼为0.16；[K_E]为单元刚度矩阵；G_E为单元结构阻尼系数，由MAT1卡片中的GE值决定，如图6.4.1所示。

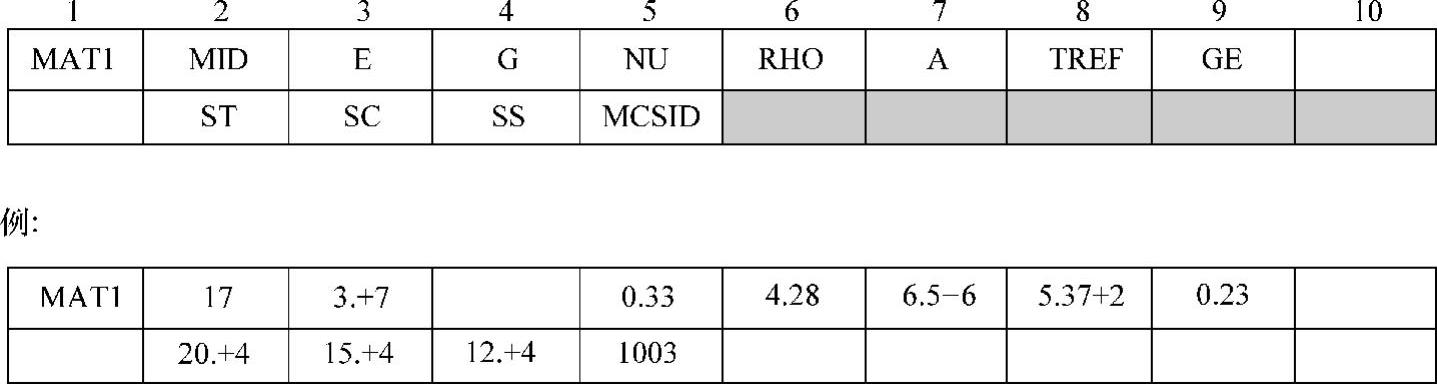
图6.4.1 MAT1卡片中的GE值

2.运动方程式求解

直接频率响应分析通过代数解法求解一系列耦合的矩阵方程，计算每个激励频率作用下的结构响应。对于简谐激励作用下的强迫运动，方程式为(www.xing528.com)

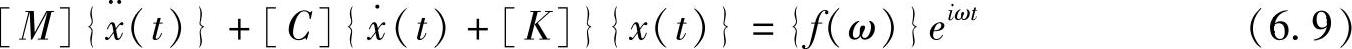
对于最基础的简谐运动，假设解为如下的简谐形式：

式中，等号右边的幅值项{u（ω）}为位移向量，是个复数。

将式（6.10）代入到式（6.9），得到：

-ω²[M]{u（ω）}e^iωt+iω[C]{u（ω）}e^iωt+[K]{u（ω）}e^iωt={f（ω）}e^iωt （6.11）

将上式简化后可以得到：

-ω²[M+iωC+K]{u（ω）}={f（ω）} （6.12）

对上式开展复数算法，就可以求解每一个激励作用下的运动方程式，从而得到方程式的解，即特征值和特征向量。