汽车NVH性能开发：模态理论基础与振动模式计算方法

结构振动问题由激励、振动结构和响应三部分组成，如果已知激励和响应，特征值求解的结果是结构的固有频率和振型，对应系统的特征值和特征向量。图6.3.1所示的单自由度振动系统，由质量、刚度、阻尼和激励构成。系统的运动方程式如式（6.4）所示。

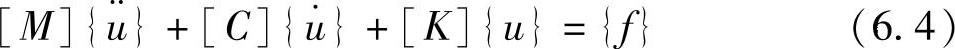
式中，[M]为系统的质量矩阵；[C]为系统的阻尼矩阵；[K]为系统的刚度矩阵；{u}为节点位移；{f}为外载荷。

所谓结构特征值问题，就是假设系统在无阻尼及无外载荷状态下求解自由振动的模态矢量。（6.4）式中的阻尼及外载荷均为0，则方程变成如下形式：

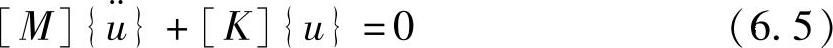
对于线弹性结构，上式中[M]、[K]均为实数对称矩阵，方

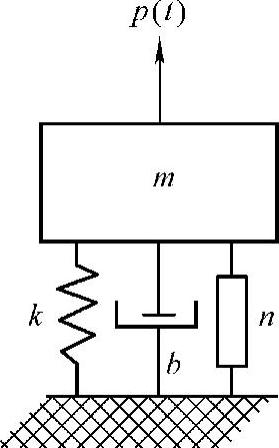
图6.3.1 单自由度模型

程具有下列简谐运动形式的解：(www.xing528.com)

式中，{ϕ}为位移矢量的幅值，它定义了位移矢量{u}的空间分布；ω_n为简谐运动的角频率。

从上式中可以求解出一系列离散的特征值ω_i。每个特征值对应三个特征向量{ϕ_i}满足运动方程式。每个特征值和特征向量决定了结构的一种自由振动模式。特征值与特征向量的数目与振动系统的自由度数相等。

对于有限元分析模型，只需指定任何单元的质量密度或NSM，软件就会自动计算质量矩阵。质量矩阵的计算有两种方法：集中质量法（lumped mass）和耦合质量法（coupled mass）。

集中质量法实际上是一种简单的静力等效计算，只需将单元的全部质量按静力等效原则分配到单元的所有节点上，然后计算质量矩阵。在这种计算中，质量只与平动自由度有关，质量矩中有关转动系数都是0。在特征值标准型的计算中，这种算法会引起奇异。

耦合质量法是按功的等效原则，根据假定位移函数由虚功原理导出，不但包括了平动惯性，还考虑了转动的惯性效应。

耦合质量法比集中质量法计算结果更精确，但集中质量法计算效率高。