快速多极边界元法解决复杂声学问题

传统边界元法虽然在多种声学问题中均有应用，但其线性代数方程组的系数矩阵是稠密且非对称满阵，求解时需要耗费巨大的计算资源。以直接边界元法为例，求解声学问题时的计算量和存储量分别与声学模型自由度呈三次方和平方的关系。此外，为了保证计算精度，边界元法要求最小分析波长内至少有6个声学单元。随着计算频域的上升，声学模型的自由度将急剧增大，导致无法正常求解。

在上述背景下，由Rokhlin提出的快速多极算法（Fast Multipole Method，FMM）结合传统边界元法的混合理论被引入到大型复杂声学问题的求解，即建立了快速多极边界元方法（Fast Multipole Boundary Element Method，FMBEM）。FMM的实质是用结点集群的多极展开式来近似表征核函数与远场边界变量乘积的边界积分，将与自由度呈三次方和平方的计算量和存储量减小到与自由度同数量级，非常适合大型复杂问题的计算。

在FMBEM的发展历程中，Greengard和Rokhlin最早推导了Helmholtz方程的多极扩展式，该理论成果后来逐渐被用于飞机、船舶、汽车、内燃机、涡轮机等大型复杂结构的声学预测中。与传统边界元“一气呵成”的求解理念不同，FMBEM将大型声学问题划分成多个计算域，每个域再进一步划分成更小的子域，最后用边界元算法求解各个子域。这种分层的结构有助于矩阵重组，从而大幅降低计算时间和内存使用。

根据声学原理，均匀理想流体介质中具有简谐解的小振幅声波波动可以用Helmholtz微分方程（式5.10）表示，该式可以在给定的边界条件下求解，如常见的Robin或阻抗边界条件、Neumann边界条件、Dirichlet边界条件等。

采用自由空间的Green函数G（x，y）对式（5.10）进行两次积分后可以推导出直接Helmholtz积分方程：

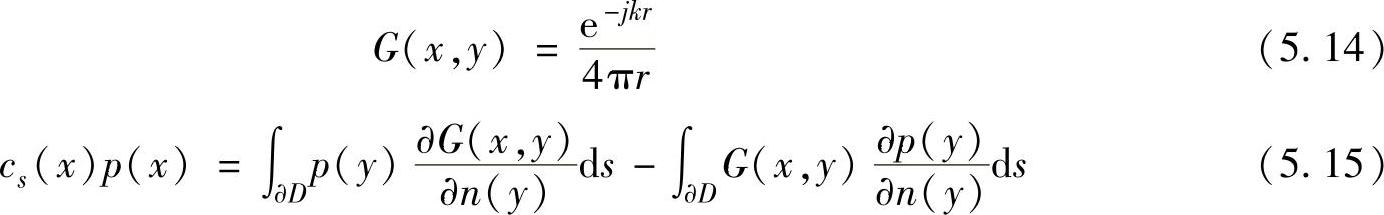
式中，r=|x-y|；c_s（x）是与点x位置相关的系数；y是声场中的观察点位置。若x在边界∂D内，c_s为1；若x在边界外，c_s为0；若x在光滑边界上，c_s为1/2。

对上式进行点x法向求导可以得到直接积分方程的法向导数形式，最终求解外声场D⁺或内声场D^-的声学响应，即直接边界元方法（Direct Boundary Element Method，DBEM）。

同理，间接Helmholtz积分方程及其法向导数形式可以用来求解整个声场D的声学响应，即间接边界元法（Indirect Boundary Element Method，IBEM），如式（5.16）和式（5.17）所示。

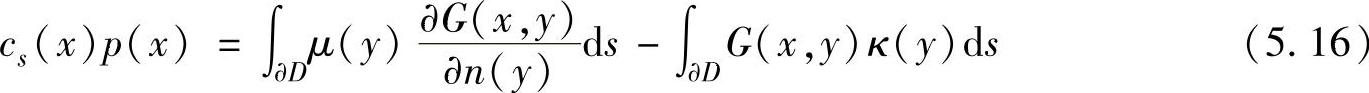
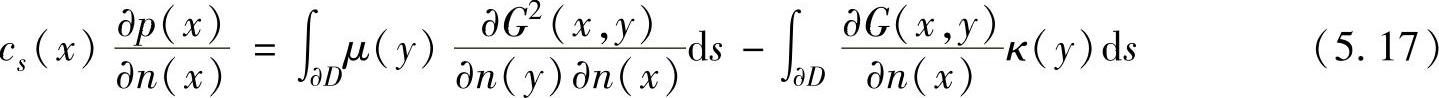
式中，μ和κ分别表示声场边界的双层势能和单层势能。

将声学模型离散成二维单元并应用每个单元节点的边界条件后，可以得到传统边界元方法的标准线性方程组：(www.xing528.com)

A·X=B （5.18）

式中，A为系数矩阵；X为未知矢量；B为已知矢量。

FMBEM可以加速式（5.16）中左项的乘积求解和整个方程组的迭代过程，这主要得益于FMM的多极扩展及转移理论。在传统边界元中，节点之间的交互作用可以用Green公式（5.14）描述，即声音的强度随着距离r的增加而减小。而FMBEM以估算的形式表示这种交互作用，如图5.3.1所示。从图中可以看到，根据Gegenbauer附加定理，Helmholtz方程的基本解可以在邻近场点y的中心y_c1点展开成多极扩展式。此外，通过多极扩展系数之间的转移，FMBEM可以估算得到另一中心场点y_c2的解。总体上来说，连接Green函数源点x和目标点y之间的向量可以划分为三个部分，它们分别是多极扩展系数向多极扩展系数的转移（Multipole-to-multipole，M2M），多极扩展系数向局部扩展系数的转移（Multipole-to-local，M2L），以及局部扩展系数向局部扩展系数转移（Local-to-local，L2L）。

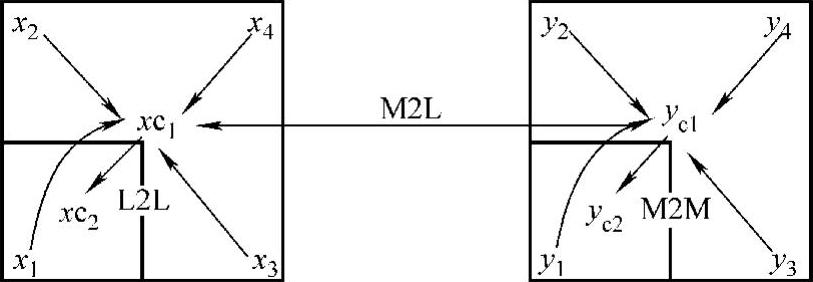
图5.3.1 快速多极边界元算法示意图

采用FMBEM计算多自由度声学问题的步骤总结如下：

1）结构边界离散化得到边界元模型，FMBEM目前适用于求解三角形声学单元。

2）生成多层八叉树结构，用来储存多极扩展系数和局部扩展系数。根据声学单元的最大单元尺寸L₀进行第一次分块，然后按第一次得到的分块再分为8个小方块（每个小方块边长为L₁=L₀/2），然后一直按照这种规则划分，进行N次后每个小方块的边长为L_N=L₀/2^N，当L_N≤λ/4之后将停止分块，其中λ为上限频率对应的波长。

3）根据递归计算的方向不同，比如母节点向上对子节点递归，或子节点向下对母节点递归，分别用于计算多极扩展系数和局部扩展系数。

4）采用传统边界元算法对树结构中各个子单元对结果进行积分求解。

5）通过迭代计算未知矢量，直到结果达到设定的精度后，求解结束并得到声学结果。