洪涝卫星遥感监测中的几何校正及精校正技术

在遥感理论中，将卫星位置和运动状态、遥感器、大气折射、地球自转、地球表面曲率、地形起伏等遥感系统内外因素影响造成的遥感图像几何位置上的变化统称为几何畸变，也就是遥感图像在几何位置上与实际地面位置有差异。在图像上表现为像元行列分布不均匀，像元大小与地面大小对应不准确等（王学平，2008）。遥感图像几何校正就是对成像过程中产生的各种畸变进行校正，得到一幅符合某种地图投影或图形表达要求的新图像，它是遥感图像处理过程中的重要环节，也是计算最为复杂和密集的部分（蒋艳凰，2004）。

（一）遥感图像几何畸变的原因

具体来说，引起遥感图像几何畸变的因素主要有以下6个方面（邵鸿飞，2000；汤竞煌，2007；杨高攀，2010）。

1.卫星位置和运动状态变化的影响

卫星围绕地球按椭圆轨道运动，引起卫星航高和飞行速度的变化，导致图像对应产生偏离与在卫星前进方向上的位置错动。另外，运动过程中卫星的偏航、翻滚和俯仰变化也能引起图像的畸变。以上误差总的来说，都是因为传感器相对于地物的位置、姿态和运动速度变化产生的，属于外部误差。

2.遥感器的影响

遥感器的影响包括扫描镜线速不均匀、扫描镜起止采样时间不同造成扫描长度的不一致，检测器采样延迟造成各个波段间的不配准与同一波段扫描之间的错动，以及全景畸变。

3.大气折射的影响

大气层属于非均匀介质，从地面往上覆盖的大气层随着高度的增加其密度递减，以大气层为传播媒介的电磁波的折射率随着大气层密度的递减而变化。当地物发出的电磁波穿越大气圈时，经折射后的传播路径不再是直线而是一条曲线。在标准的成像方式中所设计的都是直线投影成像，那么曲线成像就会造成像点位移，这也就是由于大气折射所引起的影像畸变。

4.地球自转的影响

大多数卫星都是在轨道运行的降交点接收图像，即当地球自西向东自转时，卫星自北向南运动。动态扫描传感器每条扫描带成像时间不同，造成传感器每条扫描线上的影像依次向西平移，从而使得影像产生畸变。

5.地形起伏的影响

当地形存在起伏时，使原来要反映的理想的地面点被垂直在其上的实际某高点所代替，引起图像上像点也产生相应的偏离。在影像的几何校正中特别是地形起伏较大区域要考虑利用数字高程模型或者利用含有高差修正后的模型进行影像校正。

6.地球表面曲率的影响

地球表面是不规则的曲面，这使卫星影像成像时像点发生移动，像元对应于地面的宽度不等。特别是当传感器扫描角度较大时，影响更加突出。地球曲率导致的影像畸变和地形起伏导致的像点位移类似，它主要是把地面上的点实际是球面上的点，正射到地球切平面，其中投影距离作为一种误差近似看作是地形起伏因素引起的。

（二）系统几何校正

传感器校正影像产品是针对卫星下传原始数据经过数据解扰、解密、解压、逻辑分景、辐射校正和传感器校正，但没有经过进一步几何处理的影像产品，该级产品一般附带有影像的轨道、姿态和相机模型参数文件以及DFM参数文件（类似于SPOT5的Level 1A产品以及Pleiades的Level 1产品）（周平，2015）。系统几何校正是基于传感器校正影像产品利用卫星下行的星历数据、卫星轨道和姿态数据、卫星传感器参数及预处理系统中所规定的地球模型和地图投影参数，模拟成像时卫星的状态及其视域，并产生与输出图像网格对应的重定位方程，即系统校正模型，以此为依据对影像数据进行处理的过程（刘志丽，2001）。系统几何校正是遥感卫星数据地面处理系统中不可或缺的关键一步。

系统几何校正可分为如下几个步骤（赵仕美，2016）。

（1）对获取到的卫星下行原始数据进行辅助数据分离，获取几何校正过程中所需要的行时数据、姿态数据和原始图像数据等信息。

（2）将需要进行系统几何校正的原始图像数据读入。

（3）建立校正模型，定义图像坐标与地面坐标的对应关系。

（4）根据原始图像4个角点通过校正模型确定图像输出范围，计算出输出图像的范围。

（5）根据已建立的校正模型对整幅图像进行几何校正，将像元从原始图像坐标变换到输出图像坐标；几何校正模型的建立是图像系统几何校正的基础，它定义了像素坐标和地面空间坐标数学关系。通常校正模型可分为两类：严密成像几何模型和通用成像模型。严密成像几何模型是根据不同传感器成像特性等参数而建立的校正模型，通常要考虑传感器的成像方式、卫星轨道和姿态等信息；通用成像模型则不需要考虑传感器相关参数，直接采用有理多项式等数学函数来描述像素点和相应地面点之间的关系。

（6）对输出图像的像元灰度值进行重采样。

（7）经过对逐个像元的几何位置变换和灰度重采样后，将经过几何校正后的图像输出到文件中去，完成系统几何校正处理过程。

（三）几何精校正

由传感器系统及地球曲率等引起的畸变多为系统畸变，可以通过分析传感器成像时的参数和星历数据来校正。但是系统几何校正过程中，星历数据的偏差，以及预处理系统对传感器飞行高度、姿态和速度等变化引起的随机畸变的人为假设，使得经系统校正的遥感影像仍存在着少量的内部误差和较大的定位误差，必须进行几何精校正。经过几何精校正后的卫星影像，可用于建立影像提取的信息，以及与地理信息系统或决策支持系统中其他专题信息之间建立定位关系，也可以用于提取精确的距离、多边形面积及方位等信息。在遥感影像处理中，影像几何精校正是遥感数据分析的基础，也是数据预处理的主要内容之一（侯姗姗，2010）。

几何精校正就是利用地面控制点（Ground Control Point，GCP）对各种因素引起的遥感图像几何畸变进行校正。从数学上来说，其原理是通过一组GCP建立原始的畸变图像空间与校正空间的坐标变换关系，利用这种对应关系把畸变空间中全部元素变换到校正空间中去。几何精校正步骤如下。

1.数据准备

准备待校正原始数据和参考数据，参考数据包括有高标准地理坐标的影像数据、地图资料和大地实际测量结果，控制点可从这些数据上采集或量测。

2.选择控制点

控制点选择是几何校正中最重要的一步。传统的人工选择地面控制点应当具有以下特征：首先地面控制点（GCP）在图像上有明显的、清晰的定位识别标志，如道路交叉点、河流岔口、小岛、塔、桥梁、机场跑道、铁路、水坝、建筑边界、农田界限等；其次，GCP上的地物不随时间而变化，以保证当两幅不同时段的图像或地图几何纠正时，可以同时识别出来（王姣，2006）。控制点的数量、分布和其定位精度对几何精校正精度有影响。GCP数量的增加可以提高校正精度，但也使得寻找GCP的难度加大，GCP的数量也不宜过多，因为过多不会显著提高校正精度，却使计算量大大增加；几何精校正要求GCP均匀分布，若GCP分布不均匀，则在GCP密集的区域影像校正较好，而在GCP分布稀疏的区域，则会出现较大的误差；GCP的位置精度越高，校正效果越好（赖震刚，2003）。(www.xing528.com)

计算机自动匹配选点则基于基准影像和配准影像相似性关系，基本可以分为基于灰度的匹配和基于特征的匹配。基于灰度的图像匹配算法主要有相关系数法、互信息法、傅里叶变换法、最小二乘法；基于特征的图像匹配算法主要有基于角点检测的图像配准方法和基于图像特征描述符的配准方法（熊文成，2014）。

3.建立几何校正模型

目前常用的几何校正模型有：几何多项式校正模型（Polynomial），有理函数模型（Rational Function），局部区域纠正模型（Thin Plate Spline）和严格卫星轨道模型（Rigorous Orbital Model）。这几种模型各有其特点（李立钢，2006；万里红，2007；廖文峰，2008）。

（1）几何多项式校正模型（Polynomial）。此模型基本思想是回避成像的空间几何过程，而直接对图像变形的本身进行数字模拟，认为遥感图像的整体变形可以看作是平移、缩放、旋转、仿射、偏扭、弯曲以及更高层次的基本变形的综合作用结果，因而校正前后图像相应点之间的坐标关系中可用一个适应的多项式来表达。一般多项式几何精校正算法的具体表达式（陈光洲，2014）如下：

式中，（x，y）为像点的像平面坐标；（X，Y）为其对应地面点的地面坐标。这里多项式的阶数一般不大于三次，通常讨论一般二次多项式和一般三次多项式。

一般多项式算法解算稳定，形式简单，在实际中利用率较高，适用于各种类型的传感器。此校正模型受影像覆盖面积和地形高度变化的影响，若影像覆盖面积不大且高程起伏不明显时，校正精度还可以，反之则精度明显降低。一般较适用于平地或精度要求不高的应用。此外，高阶多项式容易造成图像产生不应有的变形，需要解决几阶多项式效果最好及与控制点数的关系等问题。

（2）有理函数数学模型（Rational Function）。有理函数数学模型是一个建立像素和地面位置对应关系的简单数学模型，是对空间几何形态的直接描述。有理函数模型是用有理函数逼近二维像平面和三维物空间对应关系。有理函数正解形式表示为：

式中，（rn，cn）和（Xn，Yn，Zn）分别表示像点坐标（r，c）和地面坐标（X，Y，Z）经平移和缩放后的归一化坐标，取值位于-1.0～1.0之间。有理函数模型采用归一化坐标的目的是减少计算过程中由于数据数量级差别过大引入的舍入误差。有理函数中多项式每一项的各个坐标分量X，Y，Z的幂最大不超过3，每一项各个坐标分量幂的总和也不超过3（一般有1，2，3三种取值）。分母项p2、p4的取值可以有2种情况：p2=p4或p2≠p4。

有理函数模型不需要知道卫星轨道信息及成像参量，且其系数包含了各种因素的影响（传感器构造、地球曲率、大气折光等），因此适用于大多数传感器；但高阶有理函数模型计算复杂，通常由于参量过多会导致解的不稳定性；而且模型系数没有具体物理含义，因此校正准确度存在一定局限性。其优点在于多项式包含高程信息，在较大影像范围及地形起伏较大的情况下，可以提高校正精度。其有理函数多项式的系数可由数据生产单位在基本等级和预正射等级影像产品中直接提供RPC文件，也可以由用户自己点选控制点求得，这样精度会更高，但是需要更多的控制点。该方法缺点是需要相应地区的DEM，且在高程变化剧烈的区域精度受限。

（3）局部区域纠正模型（Thin Plate Spline）。利用控制点组成多个三角网，再分别进行每个三角形区域的多项式系数求解，然后各区域利用其各自的多项式系数进行转换。局部区域校正法的精度受控制点数量、位置及地形起伏程度等因素的影响，整体而言校正精度随控制点的增加而提高，在地形变化剧烈的地区，控制点密度还需再增加。理论上可以达到理想精度水平，但是需要数十甚至成百的控制点，校正后影像的范围为控制点确定的多边形范围，控制点多边形以外的部分被裁切，故多半用于小面积影像或局部区域修正，不适用于整景影像的校正，一般应用很少。另外，局部区域校正模型只有在其他模型校正结果不理想的情况下使用，并且其对GCP的要求比其他模型更高（蒋之富，2008）。

（4）严格卫星传感器模型（Rigorous Orbital Model）。该模型是依据传感器的成像几何关系，利用成像瞬间地面点、透视中心和相应像点3点共线的几何关系建立的数学模型，作为摄影测量学最常采用的成像模型，具有最高的定位精度，但形式较为复杂。在PCI软件中采用了加拿大国家遥感中心（CCRS）Toutin博士创造的Toutin传感器物理模型，该模型是支持QuickBird卫星影像的严格传感器模型，基于轨道学、摄影测量学、大地测量学和制图学等原理，结合成像过程中会引起几何形变的平台、传感器、地球和地图投影等因素而创建的。利用此模型结合较少的高精度GCP点和DEM数据，就可以取得很高的精度。

4.像元几何位置变换

像元几何位置变换是通过选定的某种校正模型将像元从原始影像坐标变换到输出影像坐标，通常有两种变换方式可供选择，即直接变换法和间接变换法，如图2-3所示。

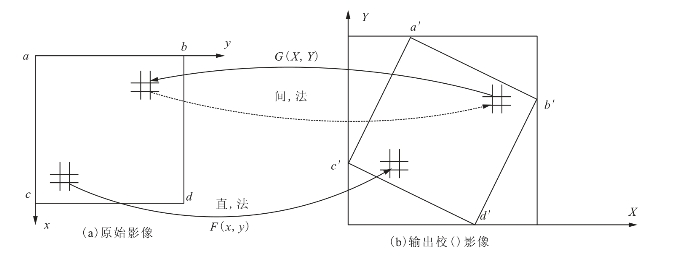
图2-3　直接变化法和间接变化法示意图（李立钢，2006）

直接变换法是从原始影像出发，依次对其中的每一像元（x，y），依据选定的校正模型F（x，y），求它在新影像中的地面坐标（X，Y），同时把（x，y）上的灰度值送到地面坐标为（X，Y）所对应的输出影像像点。间接变换法是从校正后的影像阵列出发，依次计算每个像元在原始影像中的像点位置（x，y），最后把（x，y）处灰度值赋给地面坐标为（X，Y）的输出影像像点。G（x，y）是F（x，y）的逆函数。相比较而言，直接变换法在某些校正变换中解算复杂，同时校正后的影像，有些像素可能重叠，有些像素之间可能出现空白，因此，一般很少被采用。而间接法通过灰度重采样获取校正后的像元灰度值，在实际中被广泛应用。

5.重采样

由于计算后的（x，y）多半不在原图的像元中心处，即在原始影像中的相应位置的坐标值不为整数，因此必须利用在原始影像中该点附近的若干像元的灰度，考虑这些像元对它的影响，重新计算新位置的亮度值，这个过程即称为数字图像亮度值的重采样。图像亮度值重采样时，周围像素亮度值对被采样点贡献的权可用重采样函数来表达。理想的重采样函数是辛克（SINC）函数，其横轴上各点的幅值代表了相应点对其原点处亮度贡献的权。但由于辛克函数是定义上在无穷域上的，又包括三角函数的计算，实际使用不方便，因此人们采用了一些近似函数代替它，据此产生了3种常用的重采样算法（向冬梅，2009；王运，2011；张周威，2013）。

（1）最近邻内插法。最近邻法的基本原理是：确定变换后图像上任一点（X，Y）在畸变图像上对应点的位置（i，j），比较（i，j）到邻域4个点的距离，把距离（i，j）最近的那个点的灰度值作为变换后图像上对应点的灰度值。该方法最大可产生1/2像元的位置误差，优点是输出影像仍然保持原来的像元值，处理速度快，简单易行。缺点有两个，一是会使原始图像中某些线状特征变粗成块；二是当相邻像元的灰度值相差很大时，会产生较大的误差，可能造成输出影像中某些地物的不连贯。

（2）双线性内插。使用内插点周围的4个观测点的像元值，对所求的像元值进行线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。假如想得到未知函数f在点P=（x，y）的值，假设已知函数f在Q11=（x1，y1）、Q12=（x1，y2）、Q21=（x2，y1）以及Q22=（x2，y2）4个点的值。首先在x方向进行线性插值，得到R1和R2，然后在y方向进行线性插值，得到P。双线性内插法具有平均化的低通滤波效果，边缘受到平滑作用，可以减少线状特征的块状化现象，而产生一个比较连贯的输出影像，其缺点是破坏了原来的像元值，校正后高频部分受损，图像轮廓变得模糊，在后来的波谱识别分类分析中，会引起一些问题（图2-4）。

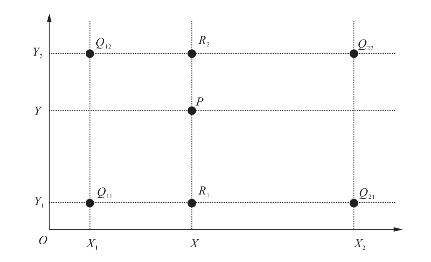
图2-4　双线性插值示意图（据叶金印，2013）

（3）三次卷积内插。其基本思想是增加邻点来获得最佳插值函数。三次卷积插值法就是S（ω）函数的近似：

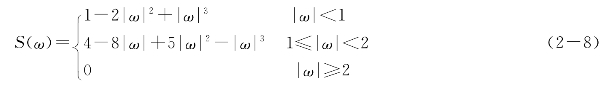
在计算时，要利用插值点周围的16个邻近点的灰度来进行。取与计算点（x，y）周围相邻的16个点，与双线性内插类似，可先在某一个方向上内插，如先在x方向上，每4个值依次内插4次，求出f（i，j-1），f（i，j），f（i，j+1），f（i，j+2），再根据这4个计算结果在y方向上内插，得到f（x，y）。每一组4个样点组成一个连续内插函数。可以证明，这种三次多项式内插过程实际上是一种卷积运算，故称为三次卷积内插。

其计算式为：

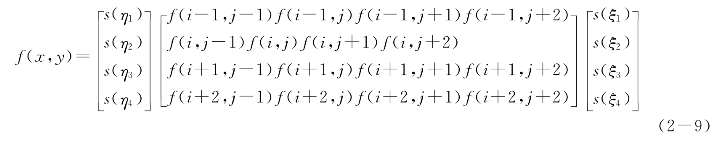
式中，ξ1=2+U，ξ2=U，ξ3=1-U，ξ4=2+U；η1=1+V，η2=V，η3=1-V，η4=2-V。U，V为共轭点离最近网格点的小数距离。

三次卷积内插法对边缘有所增强，克服最近邻法和双线性插值法的缺点，精度很高，具有图像均衡化和清晰化的效果。该方法的缺点是破坏了原来的像元值，计算量大，需耗费大量机时。