大学应用数学|假设检验的基本思想与方法

假设检验的基本思想有如下两点：

（1）为了检验一个假设是否成立，先假定其成立，再看由此会产生什么结果.如果导致了一个“不合理”的现象发生，就表明原先的假设不成立，因此应该“拒绝假设”，否则就“接受假设”.

（2）这里的“不合理”，依据的是人们在实践中广泛采用的小概率原理，即“小概率事件在一次试验中几乎不可能发生”.

我们知道，在一次试验中，如果事件A发生的概率为α，则当α很小时，事件A称为小概率事件.但α究竟为多少时，才能称为小概率，这具有相对性.在一般的生产中α=0.01或α=0.05就可以称为小概率，但如果事件的发生要影响生命、财产的安全时，就要取得更小，甚至取为α=0.000 1才可称为小概率.

下面通过实例来具体说明参数假设检验的思想和方法，并从中归纳出假设检验的基本步骤.

例9.19　某台自动包装机包装奶粉，根据长期经验知道，所装奶粉的净重服从正态分布N（500，100）.现抽取10袋，称得其重量为：512，506，508，511，504，499，507，509，498，510.试问这段时间机器工作是否正常?

解　设X表示奶粉的重量，μ，σ2分别表示这批奶粉重量X的均值和方差.根据长期经验知道方差比较稳定，于是可设X～N（μ，σ2），这里σ2已知，μ未知.

（1）提出假设H0：“μ=500”，在假设H0成立的条件下，是否会发生不合理的现象.

（2）如果假设H0成立，则有X～N（500，102），样本均值，因而统计量

（3）给定小概率α（一般取5%，1%或10%），查标准正态分布临界值表可得临界值μa/2，使，若取α=0.05，则临界值μa/2=1.96，从而，即若H0成立，则“”是一个概率仅为0.05的小概率事件.根据“小概率事件在一次试验中几乎不可能发生”的原理，我们认为在假设H0：“μ=500”成立的条件下，事件在一次试验中几乎是不可能发生的.(www.xing528.com)

（4）由样本值知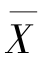=506.4，计算统计量U的实现值为因为，即上述小概率事件竟然发生了，这就表明样本的结果与假设H0不相符.所以，应拒绝假设H0，即这段时间机器工作不正常.

这里α表示样本均值和总体均值μ0=500出现差异的概率，所以α也称为显著性水平.称为检验统计量.当检验统计量在某个区城取值时，拒绝原假设H0，则称该区域为拒绝域，否则称其为接受域.如本例，对于显著性水平α=0.05，其拒绝域为（-∞，-1.96）∪（1.96，+∞），接受域为（-1.96，1.96），μa/2=1.96称为临界值.

若假设检验的拒绝域在接受域的两侧，则这类假设检验称为双侧假设检验；若假设检验的拒绝域在接受域的单侧，则这类假设检验称为单侧假设检验.

通过上述分析，将假设检验的基本步骤归纳如下：

（1）根据实际问题提出假设H0；

（2）选取适当的检验统计量，并在H0成立的前提下确定该统计量的概率分布；

（3）给定显著性水平α，由检验统计量的分布表，找出临界值，并确定拒绝域；

（4）根据样本值计算统计量的实现值，并与临界值比较，从而对接受还是拒绝H0做出判断.