参数的点估计 是θ的一个近似值.由于参数未知,无法考证估计值
是θ的一个近似值.由于参数未知,无法考证估计值 与参数θ的真值的近似程度.而在实际问题中,我们不仅需要求出参数的估计值,还要知道估计值的精确性与可靠性,即希望找出θ的一个可能的变化范围(
与参数θ的真值的近似程度.而在实际问题中,我们不仅需要求出参数的估计值,还要知道估计值的精确性与可靠性,即希望找出θ的一个可能的变化范围( ,
, ),并知道这个范围包含参数真值的可信程度.所以称这种形式的参数估计为区间估计.
),并知道这个范围包含参数真值的可信程度.所以称这种形式的参数估计为区间估计.
设θ是总体X的一个未知参数,(X1,X2,…,Xn)是来自总体X的样本,对于给定的正数α(0<α<1),若存在统计量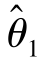 =
= (X1,X2,…,Xn)和
(X1,X2,…,Xn)和 =
=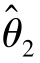 (X1,X2,…,Xn),使得
(X1,X2,…,Xn),使得
则称1-α为置信度,称区间( ,
, )为参数θ的置信度为1-α的置信区间,
)为参数θ的置信度为1-α的置信区间,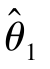 与
与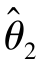 分别称为置信下限与置信上限,α称为显著性水平.
分别称为置信下限与置信上限,α称为显著性水平.
式(9.15)的直观意义是:区间( ,
,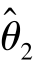 )包含未知参数θ的真值的概率为1-α.置信区间的长度,反映了精确度要求,区间越短越精确;置信度反映了区间估计的可靠性要求,α越小越可靠.
)包含未知参数θ的真值的概率为1-α.置信区间的长度,反映了精确度要求,区间越短越精确;置信度反映了区间估计的可靠性要求,α越小越可靠.
由于服从或近似服从正态分布的总体广泛存在,因此我们着重讨论正态总体期望与方差的区间估计.
1.正态总体均值μ的区间估计
设总体X~N(μ,σ2),(X1,X2,…,Xn)是来自总体X的样本.下面分两种情况求总体均值μ的置信度为1-α的置信区间.
(1)σ2已知,求μ的置信度为1-α的置信区间.因为X~N(μ,σ2),所以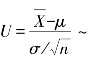 N(0,1).对于给定的α(0<α<1),令
N(0,1).对于给定的α(0<α<1),令
由此得 ,于是μ的置信区间为
,于是μ的置信区间为
其中ua/2是标准正态分布的α双侧临界值,由标准正态分布函数的定义有![]() ,据此,ua/2的值可查标准正态分布临界值表(附录5)而得.
,据此,ua/2的值可查标准正态分布临界值表(附录5)而得.
例9.16 某车间生产的零件长度服从正态分布N(μ,0.22),从当日产品中随机抽取5个,测得长度(单位:mm)分别为22.0,21.4,21.8,22.3,21.5.试求零件长度数学期望的置信度为99%的置信区间.
解 由题意知,![]() (22.0+21.4+21.8+22.3+21.5)=21.8,σ=0.2,n=5,置信度1-α=0.99,故α=0.01,查标准正态分布双侧临界值表(附录5),得ua/2=2.58,于是零件长度数学期望的置信度为99%的置信区间为:
(22.0+21.4+21.8+22.3+21.5)=21.8,σ=0.2,n=5,置信度1-α=0.99,故α=0.01,查标准正态分布双侧临界值表(附录5),得ua/2=2.58,于是零件长度数学期望的置信度为99%的置信区间为:
(2)σ2未知,求μ的置信度为1-α的置信区间.当总体的方差σ2未知时,自然想到用样本方差S2代替总体方差σ2.而 .对于给定的α(0<α<1),查t分布双侧临界值表,可求出满足
.对于给定的α(0<α<1),查t分布双侧临界值表,可求出满足![]() 的临界值λ0=tα(n-1).
的临界值λ0=tα(n-1).
例9.17 测得自动车床加工的10个零件尺寸与规定尺寸的偏差为:+2,+1,-2,+3,+2,+4,-2,+5,+3,+4,并且被测总体近似地服从正态分布.求零件尺寸偏差的数学期望的置信区间(α=0.05).
解 由所给数据得,
由于α=0.05,n=10,查自由度为9的t分布双侧临界值表,得t0.05(9)=2.262,于是(https://www.xing528.com)
即零件尺寸偏差的数学期望的置信区间(α=0.05)为(0.28,3.72).
2.正态总体方差的区间估计
因为在一般情况下总体的均值μ是未知的,所以这里只讨论当均值μ未知时,对方差σ2的区间估计,即根据样本找出σ2的置信区间.
设总体X~N(μ,σ2),(X1,X2,…,Xn)是来自总体X的样本,所以 .对于给定的α(0<α<1),查χ2分布的临界值表,选取λ1,λ2,使
.对于给定的α(0<α<1),查χ2分布的临界值表,选取λ1,λ2,使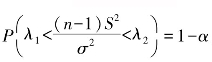 ,且满
,且满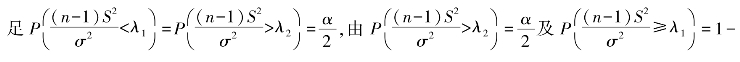
![]() ,可得
,可得![]() ,因此,方差σ2的置信度为1-α的置信区间为
,因此,方差σ2的置信度为1-α的置信区间为
而标准差σ的置信度为1-α的置信区间为
例9.18 随机地取某种炮弹9发作试验,测得炮口速度的样本标准差S=11(m/s),设炮口速度X~N(μ,σ2),求这种炮弹的炮口速度的标准差σ的置信度为95%的置信区间.
解 由置信度1-α=0.95知, ,n-1=8,查χ2分布的临界值表得,
,n-1=8,查χ2分布的临界值表得,![]() ,S=11(m/s),由式(9.19)得这种炮弹的炮口速度的标准差σ的置信度为95%的置信区间为
,S=11(m/s),由式(9.19)得这种炮弹的炮口速度的标准差σ的置信度为95%的置信区间为
练习9.2
1.设总体X具有概率密度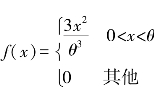 ,(X1,X2,…,Xn)为来自总体X的样本,未知参数θ>0,求θ的矩估计量.
,(X1,X2,…,Xn)为来自总体X的样本,未知参数θ>0,求θ的矩估计量.
2.设总体X服从参数为N和p的二项分布,(X1,X2,…,Xn)为取自总体X的样本,试求参数N和p的矩估计量.
3.设总体X~N(μ,σ2),(X1,X2,X3)是来自总体X的样本,试证:估计量
都是μ的无偏估计,并指出它们中哪一个最有效.
4.从大批彩色显像管中随机抽取100只,其平均寿命为10 000小时,可以认为显像管的寿命X服从正态分布.已知均方差σ=40小时,在置信度95%下求出这批显像管平均寿命的置信区间.
5.设随机地调查26年投资的年利润率(%),得样本标准差S=15(%),且投资的年利润率X服从正态分布,求它的方差的区间估计(置信度为95%).
6.生产一个零件所需时间(单位:秒)X~N(μ,σ2),观察25个零件的生产时间得 =5.5,S=1.73,试求μ和σ2的置信区间(置信度为95%).
=5.5,S=1.73,试求μ和σ2的置信区间(置信度为95%).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




