1.点估计的概念
点估计 设θ是总体X的未知参数,(X1,X2,…,Xn)是来自总体X的一个样本,(x1,x2,…,xn)是相应的样本值.所谓对参数θ作点估计,就是构造恰当的统计量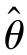 (X1,X2,…,Xn),用它的观测值
(X1,X2,…,Xn),用它的观测值 (x1,x2,…,xn)来估计未知参数θ,我们称
(x1,x2,…,xn)来估计未知参数θ,我们称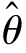 (X1,X2,…,Xn)为θ的估计量,θ^(x1,x2,…,xn)为θ的估计值,这种用
(X1,X2,…,Xn)为θ的估计量,θ^(x1,x2,…,xn)为θ的估计值,这种用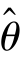 对参数θ所做的定值估计称为参数的点估计.
对参数θ所做的定值估计称为参数的点估计.
2.点估计的评价标准
当对总体的某一参数θ进行估计时,由于所采用的方法不同,因此可能存在不同的估计量.那么采用哪一个估计量为好?怎样衡量其好坏?这就涉及评价估计量好坏的标准问题.下面将介绍评价估计量好坏的两个基本标准——无偏性和有效性.
(1)无偏性.设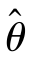 (X1,X2,…,Xn)为参数θ的估计量,若E(
(X1,X2,…,Xn)为参数θ的估计量,若E(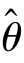 )=θ,则称
)=θ,则称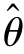 为θ的无偏估计量.
为θ的无偏估计量.
无偏性是对估计量的最基本要求.由于取值的随机性,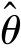 的值可能偏离参数θ的真值,但如果
的值可能偏离参数θ的真值,但如果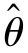 满足无偏性,
满足无偏性,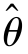 取值的平均数(即数学期望)就等于参数θ的真值.在实际中,我们通常把[E(
取值的平均数(即数学期望)就等于参数θ的真值.在实际中,我们通常把[E(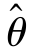 )-θ]称为以
)-θ]称为以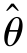 估计θ的系统误差.无偏性估计的实际意义就是无系统误差.
估计θ的系统误差.无偏性估计的实际意义就是无系统误差.
例9.10 设(X1,X2,…,Xn)是来自总体X的样本.试证明:样本均值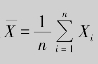 与样本方差
与样本方差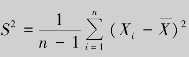 分别是总体均值与总体方差的无偏估计量.
分别是总体均值与总体方差的无偏估计量.
证明 因为Xi(i=1,2,…,n)与总体X有相同的分布,且相互独立,所以![]()
 即
即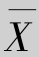 是总体均值E(X)的无偏估计量.
是总体均值E(X)的无偏估计量.
由方差的计算公式,对于随机变量X和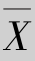 ,有
,有
即S2是总体方差D(X)的无偏估计量.
(2)有效性.用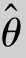 估计θ仅有无偏性是不够的,比如
估计θ仅有无偏性是不够的,比如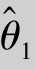 ,
,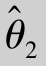 都是θ的无偏估计量,因而他们都在θ附近摆动.如果在样本容量相同的情况下,
都是θ的无偏估计量,因而他们都在θ附近摆动.如果在样本容量相同的情况下,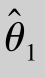 的观测值较
的观测值较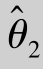 更密集在真值附近,即D(
更密集在真值附近,即D(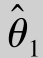 )<D(
)<D(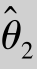 ),我们当然认为
),我们当然认为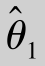 较
较 更好.所以对于θ的所有无偏估计,方差越小越好,这就是有效性的要求.
更好.所以对于θ的所有无偏估计,方差越小越好,这就是有效性的要求.
有效性 设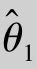 ,
,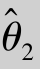 都是θ的无偏估计量,若D(
都是θ的无偏估计量,若D(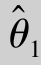 )<D(
)<D(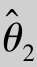 ),则称
),则称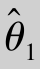 较
较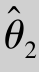 有效.
有效.
例9.11 设X1,X2是来自正态总体N(μ,1)的容量为2的样本,下列三个估计量:
哪一个更优?
解 因为![]() ,所以
,所以![]() 都是参数μ的无偏估计量;由方差的性质及D(X1)=D(X2)=1,可计算它们的方差为:
都是参数μ的无偏估计量;由方差的性质及D(X1)=D(X2)=1,可计算它们的方差为:
其中![]() 最小,所以
最小,所以![]() 比
比![]() 更有效,即
更有效,即![]() 是三个估计量中最好的一个.
是三个估计量中最好的一个.
3.求点估计量的方法
(1)数字特征法.数字特征法就是用样本的数字特征作为总体相应的数字特征的点估计量,它是求点估计量的常用方法.
以样本均值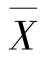 作为总体均值μ的点估计量,即
作为总体均值μ的点估计量,即
而![]() 为μ的点估计值;以样本方差S2作为总体方差σ2的点估计量,即(https://www.xing528.com)
为μ的点估计值;以样本方差S2作为总体方差σ2的点估计量,即(https://www.xing528.com)
而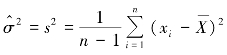 为σ2的点估计值.
为σ2的点估计值.
由前面的分析可知,样本均值和样本方差分别是总体均值和总体方差的较好的无偏估计量,在实际中经常使用它.
例9.12 已知总体X~e(λ),参数λ未知,试用数字特征法求λ的点估计量.
解 总体X~e(λ),未知参数只有一个,且有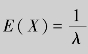 ,从而
,从而![]() ;又因为
;又因为![]() ,所以
,所以
例9.13 设总体X的分布密度为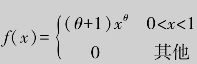 ,试求未知参数θ的点估计量.
,试求未知参数θ的点估计量.
解 这不是常见分布,但只有一个参数,可用总体的期望表示之.因为![]()
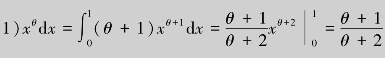 ,所以
,所以
用样本均值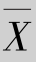 作为E(X)的点估计量,得θ的点估计量为
作为E(X)的点估计量,得θ的点估计量为
(2)矩估计法.矩是较为广泛的一种数字特征,前面讲过的数学期望与方差都是某种矩.先看看矩的定义.
矩:若E(Xk)(k=1,2,…)存在,则称E(Xk)为随机变量X的k阶原点矩;若E[XE(X)]k(k=1,2,…)存在,则称E[X-E(X)]k为随机变量X的k阶中心矩.
显然,数学期望是一阶原点矩,方差是二阶中心矩.
矩估计法就是利用样本的各阶原点矩与相应的总体矩来建立估计量应满足的方程,从而求出未知参数估计量的方法.
设(X1,X2,…,Xn)是来自总体X的样本,θ1,θ2,…,θk为总体X的k个待估参数,总体X的分布函数可以表示成F(x,θ1,θ2,…,θk).显然,总体X的前k阶原点矩aj=E(Xj)(j=1,2,…,k)也是θ1,θ2,…,θk的函数,记作
解此方程组,得
再用样本的各阶原点矩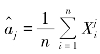 替换总体的各阶原点矩aj=E(Xj)(j=1,2,…,k)得到与参数θ1,θ2,…,θk对应的点估计量:
替换总体的各阶原点矩aj=E(Xj)(j=1,2,…,k)得到与参数θ1,θ2,…,θk对应的点估计量:
用这种方法得到的参数θ1,θ2,…,θk的点估计量![]() 称为矩估计量.
称为矩估计量.
例9.14 用矩估计法求例9.12中参数λ的矩估计量.
解 由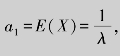 得
得![]() ,而
,而![]() ,所以λ的矩估计量为
,所以λ的矩估计量为![]() .
.
例9.15 设总体X~N(μ,σ2),且σ2>0,但μ,σ2均未知,(X1,X2,…,Xn)是来自总体X的样本,试求μ,σ2的矩估计量.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




