常用分布临界值及计算方法

概率分布临界值的概念在统计推断中有重要的作用，在参数估计和假设检验中常常用到.下面先给出临界值的定义，然后讨论几种常用分布的临界值.

临界值　对于总体X和给定的正数α（0＜α＜1），称满足条件

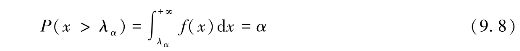
的实数λα为X分布的临界值（或上α分位点）.

1.标准正态分布的临界值

标准正态分布的临界值记为μα（图9.3），即

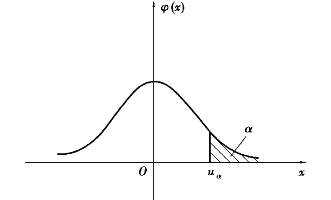
图9.3

由于Φ（x）=P（X≤x），于是

P（x＞μα）=1-P（x≤μα）=1-Φ（μα）=α

即

Φ（μα）=1-α

对给定的α，查标准正态分布临界值表（附录5）可求出μα.

例如，当α=0.025时，μ0.025=1.96；当α=0.05时，μ0.05=1.65；当α=0.95时，利用正态分布的对称性，有μα=-μ1-α，于是μ0.95=-μ0.05=-1.65.

例9.7　设总体X～N（2，52），（X1，X2，…，X10）是来自总体X的一个样本，求满足P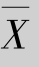（＞μα）=0.05的μα.

解　因为X～N（2，52），μ=2，σ=5，n=10，所以.又因为P，所以，于是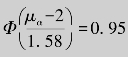，查标准正态分布表知1.65，所以μα=4.607.

2.χ2分布的临界值

自由度为n的χ2分布的临界值记为，由给定的n，α，查χ2分布临界值表（附录6），即可求得（图9.4），例如

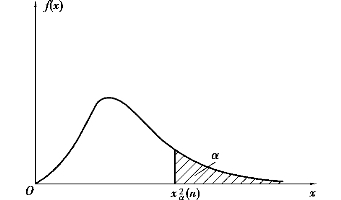
图9.4

例9.8　已知X～χ2（25），求满足P（X＞λ1）=0.01及P（X≤λ2）=0.75的λ1和λ2.

解　对于P（X＞λ1）=0.01，这里n=25，α=0.01，查附录6，得λ1=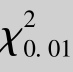（25）=44.314；

对于P（X≤λ2）=0.75，由P（X≤λ2）=1-P（X＞λ2）=0.75，得P（X＞λ2）=0.25；查附录6，得λ2=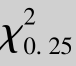（25）=29.339.(www.xing528.com)

3.t分布的临界值

t分布的临界值记为tα.由给定的α和n，通过查t分布临界值表（附录7），可求出tα（n）（图9.5）.与正态分布类似，tα=-t1-α.

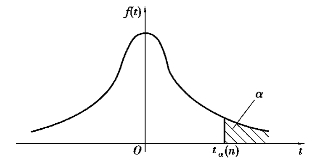
图9.5

若P（t（n）＞λ）=α，则P（t（n）＜-λ）=α，P（|（n）|＜λ）=1-2α.

例9.9　设T～t（10），求（1）α=0.05时的双侧临界值；（2）设P（t＞λ）=0.01，求λ；（3）设P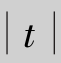（＜λ）=0.95，求λ.

解　（1）这里α=0.05，n=10，查附录7，得对应的双侧临界值λ=t0.05（10）=2.228.

（2）由P（t＞λ）=0.01知，查附录7，所求的单侧临界值λ=t0.01（10）=2.764.

（3）因为P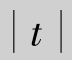（＜λ）=0.95，所以P（t＞λ）=0.025，查附录7，得对应的单侧临界值λ=t0.025（10）=2.228.

练习9.1

1.设X～N（μ，σ2），μ未知，且σ2已知，X1，…，Xn为取自此总体的一个样本，指出下列各式中哪些是统计量，哪些不是，为什么?

（1）X1+X2+Xn-μ；

（2）Xn-Xn-1；

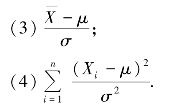
2.对某型号的木材作抗压力实验，用10个试件试验的数据为：482，493，457，471，510，446，435，418，394，469（MPa）.求这个样本的均值和方差.

3.由附录查表求下列各值：

（1）u0.05；

（3）t0.01（10），t0.9（8）；

4.设总体X～N（80，202），从总体中抽取一个容量为100的样本，问样本均值与总体均值之差的绝对值大于3的概率是多少?

5.设总体X～N（0，1），从此总体中取一个容量为6的样本（X1，…，X6），设Y=（X1+X2+X3）2+（X4+X5+X6）2，试决定常数c，使得随机变量cY服从χ2分布.

6.设总体X，Y互相独立，X～N（150，400），Y～N（125，625），现从总体中各抽取容量为5的样本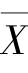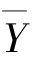，，分别为样本均值，求P（X-Y≤0）.