大学应用数学-统计量分布

1.统计量

样本是总体的代表与反映，是对总体进行分析、推断的依据.但在实际应用时，却很少直接利用样本所提供的原始数据进行推断，而是针对不同的问题构造出样本的函数，这些函数称为统计量.

统计量　设（X1，X2，…，Xn）是来自总体X的一个样本，g（X1，X2，…，Xn）是一连续函数，且不包含任何未知参数，则称g（X1，X2，…，Xn）为统计量.

因为样本（X1，X2，…，Xn）是随机变量，所以统计量也是随机变量.若样本的观测值是（x1，x2，…，xn），则g（x1，x2，…，xn）就是相应的统计量g（X1，X2，…，Xn）的观测值.

例9.3　设（X1，X2，…，Xn）是来自总体X～N（μ，σ2）的一个样本，其中μ已知而σ2未知，则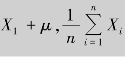均为统计量，而就不是统计量，因为它含有未知参数σ2.

统计量具有浓缩信息的作用.引进统计量后，可以把杂乱无章的许多数据整理成若干统计量的观察值，今后的统计推断往往就是建立在这些量的基础上.

2.常用的统计量及其分布

（1）样本均值、样本方差.　设（X1，X2，…，Xn）是来自总体X的一个样本，则统计量

称为样本均值.而统计量

称为样本方差.

称为样本均方差.

在实际计算中，通常采用公式

上述统计量的观察值通常用小写字母表示，如的观察值记作，即，与的称呼一致，也称为样本均值.

（2）U统计量及分布.U统计量　设（X1，X2，…，Xn）是来自总体X～N（μ，σ2）的一个样本，其中μ，σ2是已知参数，为样本均值，则称统计量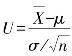为U统计量.

定理9.1　设（X1，X2，…，Xn）是来自总体X～N（μ，σ2）的一个样本，其中μ、σ2是已知参数.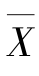 为样本均值，则

例9.4　设总体X～N（2，52），（X1，X2，…，X10）是来自总体X的一个样本，求：

解　（1）因为X～N（2，52），μ=2，σ=5，n=10，所以

（2）因为～N（2，1.582），所以

查标准正态分布表（附录4）得

Φ（0.63）=0.735 7

于是

P（1≤≤3）=2×0.735 7-1=0.471 4(www.xing528.com)

（3）χ2分布及统计量的分布.χ2分布　设（X1，X2，…，Xn）是来自总体X～N（0，1）的样本，则称统计量为自由度为n的χ2统计量，它服从的分布称为χ2分布，简记作：

χ2～χ2（n）

图9.1给出了χ2分布的概率密度f（x）当n=1，5，15时的曲线.

χ2分布与正态分布有明显的不同，它是一种不对称的分布，n是唯一参数.当n很大时（一般n＞45），其图形接近正态分布，因此χ2（n）分布表只列到n=45.

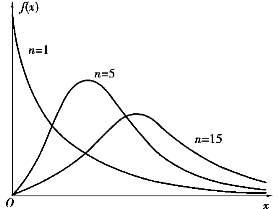
图9.1

例9.5　设（X1，X2，…，Xn）是来自总体X～N（0，1）的一个样本，Y=[（X1+X2+X3）2+（X4+X5+X6）2].证明Y～χ2（2）.

证明　由题意，Xi～N（0，1），于是

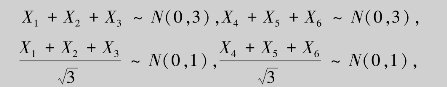
由χ2统计量的定义，得

定理9.2　设（X1，X2，…，Xn）是来自总体X～N（μ，σ2）的一个样本，则

（1）样本均值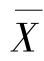与样本方差S2相互独立；

即统计量服从自由度为n-1的χ2分布.

例9.6　设（X1，X2，X3，X4）是来自总体X～N（1，25）的一个样本，则统计量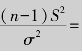

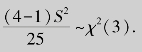
（4）t分布及统计量的分布.t统计量　设X～N（0，1），Y～χ2（n），并且X，Y相互独立，则称统计量为自由度为n的t统计量.它服从的分布称为t分布（或学生氏分布），记为t～t（n）.

图9.2给出了n=2，6，及n→+∞时t分布的概率密度f（t）的图形.t分布的概率密度f（t）有如下性质：

图9.2

（1）f（t）的图像是关于y轴对称；

（2）当n→+∞时

在实际应用中，当n≥30，t分布近似于标准正态分布N（0，1），但当n较小时，两者相差较大.

定理9.3　设（X1，X2，…，Xn）（n≥2）是来自总体X～N（μ，σ2）的一个样本，，S分别表示样本均值和样本标准差，则统计量

由此可知，凡服从t分布的统计量，其密度函数与总体的均值μ及方差σ2无关，只与样本容量n有关.