例8.37 已知两项目的基本情况如表8.4所示，试比较两项目的投资风险.
表8.4
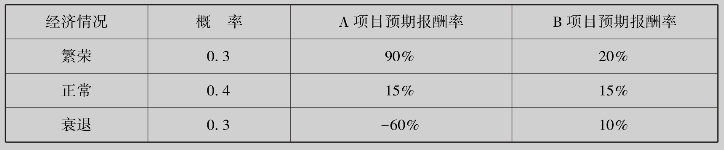
解 这是经济分析中常说的风险型决策（即在已知不同经济情况发生的概率下进行决策的问题），风险型决策的依据是：期望报酬率较高或方差更小.为此，应求两项目的期望报酬率及报酬率的方差.
A项目的期望报酬率为 E（A）=0.9×0.3+0.15×0.4+（-0.6）×0.3=15%.
B项目的期望报酬率为 E（B）=0.2×0.3+0.15×0.4+0.1×0.3=15%.
A项目报酬率的方差为
D（A）=（0.9-0.15）2×0.3+（0.15-0.15）2×0.4+（-0.6-0.15）2×0.3=33.75%.
B项目报酬率的方差为
D（B）=（0.2-0.15）2×0.3+（0.15-0.15）2×0.4+（0.1-0.15）2×0.3=0.15%.(www.xing528.com)
在两项目期望报酬率相同的情况下，A项目的方差大，即报酬率不稳定，故投资A项目的风险比B项目大.
例8.38 在产品性能试验中，如果样品报废，则企业损失2万元；如果样品试验后仍然完好，则降价处理后只损失1万元.假若样品报废和完好的概率分别是
，试求为试验该产品性能，企业平均每次支付的费用.
解 平均支付费用，就是期望值
即为试验该产品性能，企业平均每次支付费用为1.25万元.
例8.39 某服装厂准备参加某市举办的秋季服装展销会，打算租用该会陈设的摊位出售其服装产品.展销会的摊位分设于会场内三个不同的区域.展销产品收益的大小，受摊位的位置和展销期间天气的影响.根据过去资料估计，展销时间天气属于晴朗、多云、多雨三种情况的概率分别是0.35，0.40，0.25；如选A区展销，天气晴朗、多云或多雨时，可获利润分别为4 000元、6 000元或1 000元；如选B区展销，天气晴朗、多云或多雨时，可获利润分别为5 000元、4 000元或1 100元；如选C区展销，天气晴朗、多云或多雨时，可获利润分别为4 000元、3 000元或2 000元.问在上述情况下，该厂应选择哪个区域摊位展销服装产品?
解 三种方案的期望利润分别为：
E（A）=4 000×0.35+6 000×0.40+1 000×0.25=4 050元；
E（B）=5 000×0.35+4 000×0.40+1 100×0.25=3 625元；
E（C）=4 000×0.35+3 000×0.40+2 000×0.25=3 100元.
比较三种方案的期望利润可知，以租用A区摊位展销产品期望利润最多，可选此方案作为最优决策方案.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
